
分析 设再经过x分钟,时针与分针的夹角是90°,则分针转了6x°,时针转了$\frac{1}{2}$x°,由开始时刻钟面角为120°,结合钟面角=开始角度-时针旋转的角度+时针旋转的角度,可得出关于x的一元一次方程,解方程即可得出结论.
解答 解:4点整时,分钟与时针的夹角为30°×4=120°.
设再经过x分钟,时针与分针的夹角是90°,则分针转了6x°,时针转了$\frac{1}{2}$x°,
由已知得:120-6x+$\frac{1}{2}$x=90,
解得:x=$\frac{60}{11}$.
故答案为:4;$\frac{60}{11}$.
点评 本题考查了一元一次方程的应用以及钟面角,解题的关键是得出关于x的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系得出方程(或方程组)是关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
 如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.
如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
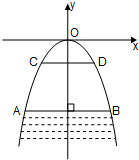 有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.
有一座抛物线形拱桥,以坐标原点O为抛物线的顶点,以y轴为抛物线的对称轴建立如图所示的坐标系,桥下面在正常水位AB时,宽20米,水位上升3米就达到警戒线CD,这时水面宽为10米.求抛物线的解析式及警戒线CD到拱桥顶O的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com