
 如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A、点B,点A的坐标为(3,0),且∠OAB=30°,点C为线段AB上一动点,过点C作CD⊥x轴,垂足为点D.
如图,在平面直角坐标系中,直线l与x轴、y轴分别交于点A、点B,点A的坐标为(3,0),且∠OAB=30°,点C为线段AB上一动点,过点C作CD⊥x轴,垂足为点D.分析 (1)先确定出OB,即可得到点B坐标,从而确定出直线l的解析式;
(2)设出点C的坐标,利用梯形的面积公式确定出点C的坐标即可确定出函数关系式;
(3)因为∠AOB=90°,所以以P,O,B为顶点的三角形与△OBA相似需分三种情况进行讨论:
①当∠OBP=90°时,又分△BPO∽△OAB;△BOP∽△OAB;
②当∠OPB=90°时,过点O作OP⊥BC于点P,过点P作PM⊥OA于点M.又分△PBO∽△OBA;△POB∽△OBA;
③当∠POB=90°时,点P在x轴上,不符合要求.
解答 解:(1)∵点A的坐标为(3,0),
∴OA=3,
在Rt△OAB中,∠OAB=30°,OA=3,
∴OB=$\sqrt{3}$,
∴B(0,$\sqrt{3}$),
设直线l解析式为y=kx+$\sqrt{3}$,
∴3k+$\sqrt{3}$=0,
∴k=-$\frac{\sqrt{3}}{3}$,
∴直线l解析式为y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$;
(2)由(1)知,直线l解析式为y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$;
∵点C为线段AB上一动点,
∴设C(m,-$\frac{\sqrt{3}}{3}$m+$\sqrt{3}$),(0<m<3),
∵S梯形OBCD=$\frac{4}{3}$$\sqrt{3}$,
∴S梯形OBCD=$\frac{1}{2}$(OB+CD)×OD=$\frac{1}{2}$($\sqrt{3}$-$\frac{\sqrt{3}}{3}$m+$\sqrt{3}$)m=$\frac{4}{3}$$\sqrt{3}$,
∴m=4(舍)或m=2,
∴C(2,$\frac{\sqrt{3}}{3}$),
∴经过点C的反比例函数解析式为y=$\frac{2\sqrt{3}}{3x}$;
(3)以P,O,B为顶点的三角形与△OBA相似时,分三种情况:
①当∠OBP=90°时,如图1,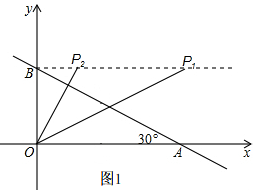 .
.
若△BPO∽△OAB,则∠BPO=∠OAB=30°,BP=$\sqrt{3}$OB=3,
∴P1(3,$\sqrt{3}$);
若△BOP∽△OAB,则∠BOP=∠OAB=30°,BP=$\frac{\sqrt{3}}{3}$OB=1,
∴P2(1,$\sqrt{3}$);
②当∠OPB=90°时,如图2.
过点O作OP⊥BA于点P,过点P作PM⊥OA于点M.
若△PBO∽△OBA,则∠BOP=∠BAO=30°,
在Rt△PBO中,BP=$\frac{1}{2}$OB=$\frac{\sqrt{3}}{2}$,OP=$\sqrt{3}$BP=$\frac{3}{2}$.
∵在Rt△PMO中,∠OPM=30°,
∴OM=$\frac{1}{2}$OP=$\frac{3}{4}$,PM=$\sqrt{3}$OM=$\frac{3\sqrt{3}}{4}$,
∴P3($\frac{3}{4}$,$\frac{3\sqrt{3}}{4}$);
若△POB∽△OBA,则∠OBP=∠BAO=30°,∠POM=30°.
∴PM=$\frac{\sqrt{3}}{3}$OM=$\frac{\sqrt{3}}{4}$,
∴P4($\frac{3}{4}$,$\frac{\sqrt{3}}{3}$);
③当∠POB=90°时,点P在x轴上,不符合要求.
综合所述,符合条件的点有四个,分别是:P1(3,$\sqrt{3}$),P2(1,$\sqrt{3}$),P3($\frac{3}{4}$,$\frac{3\sqrt{3}}{4}$),P4($\frac{3}{4}$,$\frac{\sqrt{3}}{4}$).
点评 此题是反比例函数综合题,主要考查了待定系数法求一次函数的解析式和反比例函数解析式,梯形的面积,解直角三角形,相似三角形的有关知识,难度适中.运用分类讨论、数形结合、方程思想是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,弦AB∥弦CD,∠A=28°,∠B=45°,$\widehat{ABD}$=3$\widehat{BD}$,求$\widehat{DE}$的度数.
如图,在⊙O中,弦AB∥弦CD,∠A=28°,∠B=45°,$\widehat{ABD}$=3$\widehat{BD}$,求$\widehat{DE}$的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
一个多边形的每一个内角为108°,则这个多边形是______边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com