练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．计算题：
    （1）2a2•3a2+a8÷a4-（-a）4；
    （2）（3ab）2÷（-ab）+（a-2b）2-（a+2b）（a-2b）．

    分析 （1）原式利用单项式乘以单项式法则，同底数幂的除法法则，以及积的乘方运算法则计算，合并即可得到结果；
    （2）原式利用积的乘方运算法则，完全平方公式，以及平方差公式计算即可得到结果．

    解答 解：（1）原式=6a4+a4-a4=6a4；
    （2）原式=-9ab+a2-4ab+4b2-a2+4b2=-13ab+8b2．

    点评 此题考查了整式的混合运算，完全平方公式，以及平方差公式，熟练掌握公式及运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．在平面直角坐标系中，点Q为坐标系上任意一点，某图形上的所有点在∠Q的内部（含角的边），这时我们把∠Q的最小角叫做该图形的视角．如图1，矩形ABCD，作射线OA，OB，则称∠AOB为矩形ABCD的视角．

    （1）如图1，矩形ABCD，A（-$\sqrt{3}$，1），B（$\sqrt{3}$，1），C（$\sqrt{3}$，3），D（-$\sqrt{3}$，3），直接写出视角∠AOB的度数；
    （2）在（1）的条件下，在射线CB上有一点Q，使得矩形ABCD的视角∠AQB=60°，求点Q的坐标；
    （3）如图2，⊙P的半径为1，点P（1，$\sqrt{3}$），点Q在x轴上，且⊙P的视角∠EQF的度数大于60°，若Q（a，0），求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

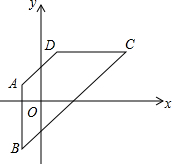    14．如图所示，四边形ABCD的四个顶点A、B、C、D的坐标分别为（-1，1）、（-1，-3）、（5，3）、（1，3），则其对称轴的函数表达式为y=-x+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，正方形网格中的每个小正方形的边长都是1，每个顶点叫作格点．
    （1）在图1中以格点为顶点画一个面积为5的正方形；
    （2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为1，3，$\sqrt{10}$，并求该三角形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．一个等腰三角形的顶角是120°，则它的底角度数是（　　）
    A．30°B．45°C．60°D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．下列实数中，是无理数的为（　　）
    A．3.14B．$\frac{1}{3}$C．$\sqrt{9}$D．$\sqrt{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

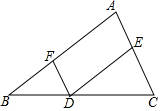    15．完成下面的证明．
    如图，点D、E、F分别是三角形ABC的边BC、CA、AB上的点，DE∥BA，DF∥CA．
    求证：∠A+∠B+∠C=180°
    证明：∵DE∥BA
    ∴∠FDE=∠BFD（两直线平行，内错角相等）
    ∴∠B=∠EDC（两直线平行，同位角相等）
    ∵DF∥CA
    ∴∠A=∠BFD，∠C=BDF（两直线平行，同位角相等）
    ∴∠A=∠FDE
    ∵∠FDE+∠CDE+∠BDF=180°（平角的定义）
    ∴∠A+∠B+∠C=180°（等量代换）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，半圆O2，半圆O3，…，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第101秒时，点P的坐标是（101，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，AC∥ED，AB∥FD，∠A=64°，则∠EDF的度数为64°．

    查看答案和解析>>

    同步练习册答案