
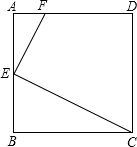
 如图,已知正方形ABCD中,AB=a,点E为AB的中点,点F在AD边上,且AF=$\frac{1}{4}$AD,试说明EF⊥CE.
如图,已知正方形ABCD中,AB=a,点E为AB的中点,点F在AD边上,且AF=$\frac{1}{4}$AD,试说明EF⊥CE. 分析 先求得AF、EB的长,然后依据两边对应成比例且夹角相等的两个三角形相似可证明△AFE∽△BEC,由相似三角形的性质可得到∠AEF=∠BCE,然后证明∠AEF+∠BEC=90°,从而可求得∠FEC=90°.
解答 解:∵ABCD为正方形,
∴AB=BC=AD=a,∠A=∠B=90°.
∵AF=$\frac{1}{4}$AD,
∴AF=$\frac{1}{4}$a.
∵E是AB的中点,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$a.
∴$\frac{AF}{AE}=\frac{BE}{BC}$.
又∵∠A=∠B,
∴△AFE∽△BEC.
∴∠AEF=∠BCE.
∵∠BEC+∠BCE=90°,
∴∠BEC+∠AEF=90°.
∴∠FEC=90°.
∴EF⊥EC.
点评 本题主要考查的是正方形的性质、相似三角形的性质和判定,证得△AFE∽△BEC是解题的关键.


科目:初中数学 来源: 题型:填空题
 QQ好友的等级会用一些图标来表示,如图是小明同学的两个好友的等级示例,小明想知道一个太阳
QQ好友的等级会用一些图标来表示,如图是小明同学的两个好友的等级示例,小明想知道一个太阳  和一个月亮
和一个月亮 所表示的等级.
所表示的等级.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
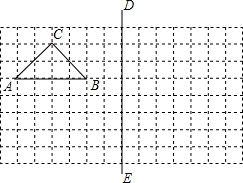 如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网络图(每小格均为边长是1的正方形)中完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?
如图,△ABC中,∠C=90°,AC=3cm,BC=6cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CBA与C、P、Q三点构成的三角形相似,求所需要的时间是多少秒?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com