
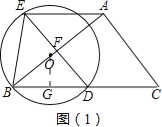
【题目】在Rt△ABC中,∠BAC=90°,BC=10,tan∠ABC=![]() ,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
,点O是AB边上的动点,以O为圆心,OB为半径的⊙O与边BC的另一交点为D,过点D作AB的垂线,交于点E,连结BE、AE.
(1)当AE∥BC(如图(1))时,求⊙O的半径;
(2)设BO=x,AE=y,求y关于x的函数关系式;
(3)若以A为圆心的⊙A与⊙O有公共点D、E,当恰好也过点C时,求DE的长.

【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]() 或12
或12
【解析】试题(1)过点O作OG⊥BD于G,设AB与DE的交点为F,如图(1),易证△AEF≌△BDF及四边形AEDC是平行四边形,从而可得BD=DC=5,根据垂径定理可得BG=DG=BD=,然后在Rt△BGO中运用三角函数和勾股定理即可求出⊙O的半径长;
(2)过点A作AH⊥BC于H,如图(2),运用三角函数、勾股定理及面积法可求出AC、AB、AH、BH、CH,根据垂径定理可得DF=EF,再根据线段垂直平分线的性质可得AE=AD.然后在Rt△BGO中运用三角函数和勾股定理可求出BG(用x的代数式表示),进而可用x的代数式依次表示出BD、DH,AD、AE,问题得以解决;
(3)①若点D在H的左边,如图(2),根据等腰三角形的性质可得DH=CH,从而依次求出BD、DF、DE的长;②若点D在H的右边,则点D与点C重合,从而可依次求出BD、DF、DE的长.
解:(1)过点O作OG⊥BD于G,设AB与DE的交点为F,如图(1),
根据垂径定理可得BG=DG.
∵AE∥BC,∴∠AEF=∠BDF.
在△AEF和△BDF中,
![]() ,
,
∴△AEF≌△BDF,
∴AE=BD.
∵∠BFD=∠BAC=90°,
∴DE∥AC.
∵AE∥BC,
∴四边形AEDC是平行四边形,
∴AE=DC,
∴BD=DC=BC=5,
∴BG=DG=BD=.
在Rt△BGO中,
tan∠OBG=![]() =,
=,
∴OG=BG=×=![]() ,
,
∴OB=![]() =
=![]() =
=![]() ,
,
∴⊙O的半径长为![]() ;
;
(2)过点A作AH⊥BC于H,如图(2),
在Rt△BAC中,
tan∠ABC=![]() =,
=,
设AC=3k,则AB=4k,
∴BC=5k=10,
∴k=2,
∴AC=6,AB=8,
∴AH=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() =
=![]() ,
,
∴HC=BC﹣BH=10﹣![]() =
=![]() .
.
∵AB⊥DE,
∴根据垂径定理可得DF=EF,
∴AB垂直平分DE,
∴AE=AD.
在Rt△BGO中,
tan∠OBG=![]() =,
=,
∴OG=BG,
∴OB=![]() =
=![]() =BG=x,
=BG=x,
∴BG=x,
∴BD=2BG=![]() ,
,
∴DH=BH﹣BD=![]() ﹣x,
﹣x,
∴y=AE=AD=![]()
=![]()
=![]() (0<x≤
(0<x≤![]() );
);
(3)①若点D在H的左边,如图(2),
∵AD=AC,AH⊥DC,
∴DH=CH=![]() ,
,
∴BD=BH﹣DH=![]() ﹣
﹣![]() =
=![]() .
.
在Rt△BFD中,
tan∠FBD=![]() =,
=,
∴BF=DF,
∴BD=![]()
=![]()
=DF=![]() ,
,
∴DF=![]() ,
,
∴DE=2DF=![]() ;
;
②若点D在H的右边,
则点D与点C重合,
∴BD=BC=10,
∴DF=10,
∴DF=6,
∴DE=2DF=12.
综上所述:当⊙A恰好也过点C时,DE的长为![]() 或12.
或12.



 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
【题目】四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装80台空调,乙安装队提前一天开工,最后与甲安装队恰好同时完成安装任务.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装多少台空调.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月销售216辆.
(1)求该品牌电动车销售量的月平均增长率;
(2)若该品牌电动自行车的进价为2300元,售价2800元,则该经销商1月至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
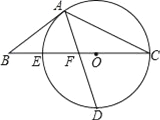
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
求证:(1)M为BD的中点;(2)![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com