
【题目】如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
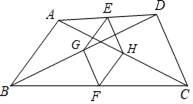
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用EG是△ABD的中位线,EH是△ADC的中位线,则有EG=![]() AB,EH=
AB,EH=![]() CD,又AB=CD,可证EG=EH,即可解题.
CD,又AB=CD,可证EG=EH,即可解题.
(2)首先运用三角形中位线定理可得到EG∥AB,HF∥AB,EH∥CD,FE∥DC,从而再根据平行于同一条直线的两直线平行得到GF∥EH,GE∥FH,可得到GFHE是平行四边形,再运用三角形中位线定理证明邻边相等,从而证明它是菱形.
解:证明:(1)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,EH是△ADC的中位线,
∴EG=![]() AB,EH=
AB,EH=![]() CD,
CD,
∵AB=CD,
∴EG=EH;
(2)∵四边形ABCD中,点F、E、G、H分别是BC、AD、BD、AC的中点,
∴EG∥AB,HF∥AB,EH∥CD,FE∥DC,
∴GF∥EH,GE∥FH(平行于同一条直线的两直线平行);
∴四边形GFHE是平行四边形,
∵四边形ABCD中,点E、F、G、H分别是BC、AD、BD、AC的中点,
∴EG是△ABD的中位线,GF是△BCD的中位线,
∴GE=![]() AB,GF=
AB,GF=![]() CD,
CD,
∵AB=CD,
∴GE=GF,
∴四边形EHFG是菱形.


科目:初中数学 来源: 题型:
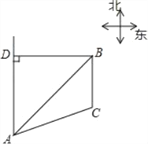
【题目】已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)(参考数据:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形土地上,修筑横向、纵向道路各一条,且它们互相垂直,若纵向道路的宽是横向道路的宽的2倍,要使剩余土地的面积为504平方米,求横向道路的宽为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
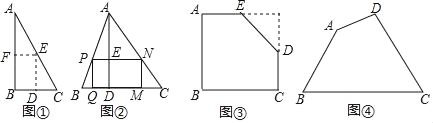
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A表示数字6,点B表示数字﹣4
(1)画数轴,并在数轴上标出点A与点B;
(2)数轴上一动点C从点A出发,沿数轴的负方向以每秒2个单位长度的速度移动,经过4秒到达点E,数轴上另一动点D从点B出发,沿数轴的正方向以每秒1个单位长度的速度移动,经过8秒到达点F,求出点E与点F所表示的数,并在第(1)题的数轴上标出点E,点F;
(3)在第(2)题的条件下,在数轴上找出点H,使点H到点E距离与点H到点F距离之和为8,请在数轴上直接标出点H.(不需写出求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
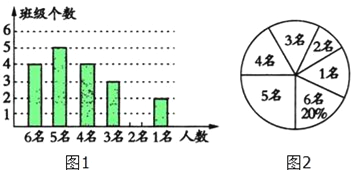
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
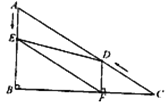
【题目】如图,在Rt△ABC中,∠B=90°,AB=5,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com