
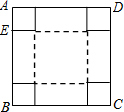
 某数学兴趣小组想用一张边长为20cm的正方形纸片ABCD(如图),制作一个无盖长方体盒子,设剪去的小正方形的边长AE=xcm.
某数学兴趣小组想用一张边长为20cm的正方形纸片ABCD(如图),制作一个无盖长方体盒子,设剪去的小正方形的边长AE=xcm.分析 (1)先利用正方形纸片ABCD的边长为20cm以及剪去的小正方形的边长AE=xcm,得出无盖长方体盒子底面的边长,再根据长方体的侧面积为128cm2列出方程,解方程即可求出x的值;
(2)首先表示出长方体盒子侧面积S与x的函数解析式,求出x的取值范围,再根据二次函数的性质即可求解.
解答 解:(1)∵剪去的小正方形的边长AE=xcm,
∴无盖长方体盒子底面的边长为(20-2x)cm.
由题意得,4(20-2x)x=128,
解得x1=2,x2=8.
所以,长方体的侧面积为128cm2时,x的值为2或8;
(2)由题意得,S=4(20-2x)x(0<x≤4),
整理得,S=-8x2+80x=-8(x-5)2+200,
∵a=-8<0,抛物线开口向下,对称轴为直线x=5,
∴当x<5时,S的值随x的增大而增大,
∴当0<x≤4时,S的最大值在x=4时取得,
∴S最大值=-8(4-5)2+200=192.
故制作成的长方体盒子侧面积S的最大值是192cm2.
点评 本题考查了二次函数的应用,一元二次方程的应用.求最值问题常利用函数的增减性来解答,注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=$-\frac{b}{2a}$时取得.


科目:初中数学 来源: 题型:选择题
| A. | 了解光明中学901班同学每周体育锻炼的时间 | |
| B. | 安踏鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 咸丰民中招聘教师,对应聘人员面试 | |
| D. | 调查光明中学683名学生的身高 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全市中学生的上网时间 | |
| B. | 检测一批灯管的使用寿命 | |
| C. | 了解神舟飞船的设备零件的质量状况 | |
| D. | 了解某品牌食品的色素添加情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com