
【题目】如图,点P是![]() 内任意一点,
内任意一点,![]() ,点M和点N分别是射线OA和射线OB上的动点,
,点M和点N分别是射线OA和射线OB上的动点,![]() 周长的最小值是5cm,则
周长的最小值是5cm,则![]() 的度数是
的度数是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=DM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出![]() 证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
分别作点P关于OA、OB的对称点![]() ,连接CD,
,连接CD,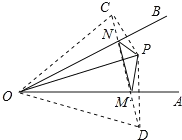
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴![]()
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴![]()
∴![]()
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE= °
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).

查看答案和解析>>
科目:初中数学 来源: 题型:
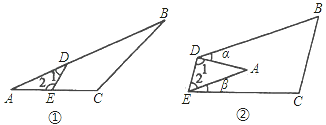
【题目】(1)如图①所示,∠1+∠2与∠B+∠C有什么关系?为什么?
(2)如图②若把△ABC纸片沿DE点折叠当点A落在四边形BCED内部时,则∠A与∠α+∠β之间有一种数量关系始终保持不变,请写出这个规律并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的底边BC=10cm,当BC边上的高线AD从小到大变化时,△ABC的面积也随之变化.
(1)在这个变化过程中,自变量和因变量各是什么?
(2)△ABC的面积S(cm2)与高线h(cm)之间的关系式是什么?
(3)用表格表示当h由4cm变到10cm时(每次增加1cm),S的相应值;
(4)当h每增加1cm时,S如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④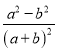 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
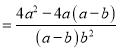
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com