
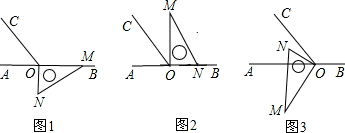
分析 (1)根据旋转的性质知,旋转角是∠MON;
(2)①如图3,利用平角的定义,结合已知条件“∠AOC:∠BOC=1:2”求得∠AOC=60°,进而得出∠AON=30°,∠AOM=60°,根据旋转的性质即可求得旋转角度为150°;
②由∠AOM=90°-∠AON,∠NOC=60°-∠AON,即可推知∠AOM-∠NOC=30°.
解答 解:(1)由旋转的性质知,旋转角∠MON=90°.
故答案是:90;
(2)①如图3,设∠AOC=α,由∠AOC:∠BOC=1:2可得∠BOC=2α.
∵∠AOC+∠BOC=180°,
∴α+2α=180°.
解得 α=60°.
即∠AOC=60°.
当三角板的直角边ON恰好平分∠AOC时,∠AON=30°,
∴∠AOM=60°,
∴旋转角度为:90°+60°=150°;
故答案为:150;
②∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON,∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.
故∠AOM-∠NOC=30°.
点评 本题综合考查了旋转的性质,角的计算.认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键..


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com