
【题目】在平面上,对于给定的线段AB和点C,若平面上的点P(可以与点C重合)满足,∠APB=∠ACB.则称点P为点C关于直线AB的联络点.

在平面直角坐标系xOy中,已知点A(2,0),B(0,2),C(﹣2,0).
(1)在P1(2,2),P(1,0),R(1+![]() ,1)三个点中,是点O关于线段AB的联络点的是 .
,1)三个点中,是点O关于线段AB的联络点的是 .
(2)若点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求点P的横坐标m的取值范围;
(3)直线y=x+b(b>0)与x轴,y轴分交于点M,N,若在线段BC上存在点N关于线段OM的联络点,直接写出b的取值范围.
【答案】(1)P1,R.(2)1﹣![]() ≤m≤1+
≤m≤1+![]() ;(3)1≤b≤2.
;(3)1≤b≤2.
【解析】
(1)根据点P为点C关于直线AB的联络点的定义一一判断即可.
(2)如图2中,作△AOB的外接圆⊙E,过点E作x轴的平行线交⊙E于G,H.首先说明当点P在优弧![]() 上时,点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求出G,H的坐标即可解决问题.
上时,点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求出G,H的坐标即可解决问题.
(3)如图3中,作△MON的外接圆⊙E,作点E关于X轴的对称点E′,以E′为圆心,OE′为半径作⊙E′.观察图象可知满足条件的点P在两个圆的优弧OM上,当⊙E与AB相切时,切点为H,求出点H的坐标即可判断.
解:(1)如图1中,
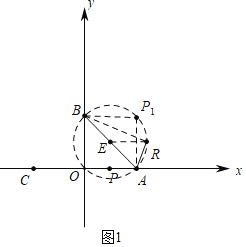
∵A(2,0),B(0,2),P1(2,2),P(1,0),R(1+![]() ,1),
,1),
∴OA=OB=AP1=BP1,
∴四边形OAP1B是菱形,
∵∠AOB=90°,
∴四边形OAP1B是正方形,
∴∠AP1B=∠AOB=90°,
∴P1是点O关于线段AB的联络点,
∵AB=2![]() ,取AB的中点E(1,1),
,取AB的中点E(1,1),
∵ER=![]() =BE=AE,
=BE=AE,
∴∠ARB=90°=∠AOB,
∴点R是点O关于线段AB的联络点,
故答案为P1,R.
(2)如图2中,作△AOB的外接圆⊙E,过点E作x轴的平行线交⊙E于G,H.
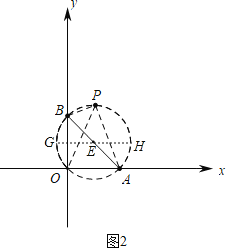
∵∠APB=∠AOB=90°,∠APO=∠ABO=45°,
∴当点P在优弧![]() 上时,点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,
上时,点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,
∵AB=2![]() ,E(1,1),G(1﹣
,E(1,1),G(1﹣![]() ,1),H(1+
,1),H(1+![]() ,1)
,1)
∴点P的横坐标m的取值范围1﹣![]() ≤m≤1+
≤m≤1+![]() .
.
(3)如图3中,作△MON的外接圆⊙E,作点E关于X轴的对称点E′,以E′为圆心,OE′为半径作⊙E′.
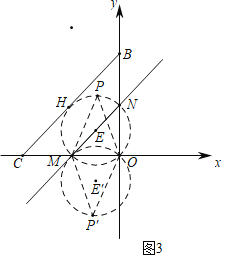
观察图象可知满足条件的点P在两个圆的优弧OM上,
当⊙E与AB相切时,切点为H,由题意⊙E的直径为![]() ,
,
∴MN=![]() ,
,
∵OM=ON,∠MON=90°,
∴ON=1,此时直线MN的解析式为y=x+1,
观察图象可知:若在线段BC上存在点N关于线段OM的联络点,则b的取值范围为1≤b≤2.


科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
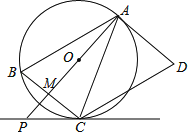
(1)求证:∠BAP=∠CAP;
(2)判断直线PC与⊙O的位置关系,并说明理由;
(3)若AB=5![]() ,BC=10,求PC的长.
,BC=10,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”号召,某校开展了志愿者服务活动,活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项,活动期间,随机抽取了部分学生对志愿者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图.

(1)被随机抽取的学生共有多少名?
(2)在扇形统计图中,求活动数为3项的学生所对应的扇形圆心角的度数,并补全折线统计图;
(3)该校共有学生2000人,估计其中参与了4项或5项活动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年度双十一在九龙坡区杨家坪的各大知名商场举行“国产家用电器惠民抢购日”优惠促销大行动,许多家用电器经销商都利用这个契机进行打折促销活动.商社电器某国产品牌经销商的某款超高清大屏幕![]() 液晶电视机每套成本为4000元,在标价6000元的基础上打9折销售.
液晶电视机每套成本为4000元,在标价6000元的基础上打9折销售.
(1)现在该经销商欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于![]() ?
?
(2)据媒体爆料,有一些经销商先提高商品价格后再降价促销,存在欺诈行为.重百电器另一个该品牌的经销商也销售相同的超高清大屏幕![]() 液晶电视机,其成本、标价与商社电器的经销商一致,以前每周可售出20台,现重百的经销商先将标价提高
液晶电视机,其成本、标价与商社电器的经销商一致,以前每周可售出20台,现重百的经销商先将标价提高![]() ,再大幅降价
,再大幅降价![]() 元,使得这款电视机在2019年11月11日那一天卖出的数量就比原来一周卖出的数量增加了
元,使得这款电视机在2019年11月11日那一天卖出的数量就比原来一周卖出的数量增加了![]() ,这样一天的利润达到22400元,求
,这样一天的利润达到22400元,求![]() 的值.(利润=售价-成本)
的值.(利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是半圆O上的一点,AB是⊙O的直径,D是![]() 的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
的中点,作DE⊥AB于点E,连接AC交DE于点F,求证:AF=DF.
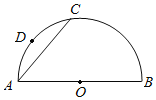
下面是小明的做法,请帮他补充完整(包括补全图形)
解:补全半圆O为完整的⊙O,连接AD,延长DE交⊙O于点H(补全图形)
∵D是![]() 的中点,
的中点,
∴![]() .
.
∵DE⊥AB,AB是⊙O的直径,
∴![]() ( )(填推理依据)
( )(填推理依据)
∴![]()
∴∠ADF=∠FAD( )(填推理依据)
∴AF=DF( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△BCD中,DF⊥BC于点F,点A为直线DF上一动点,以B为旋转中心,把BA顺时针方向旋转60°至BE,连接EC.
(1)当点A在线段DF的延长线上时,
①求证:DA=CE;
②判断∠DEC和∠EDC的数量关系,并说明理由;
(2)当∠DEC=45°时,连接AC,求∠BAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
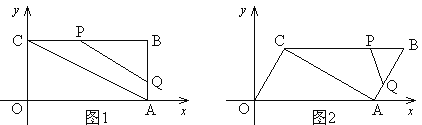
【题目】在平面直角坐标系中,O为原点,四边形OABC的顶点A在![]() 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥![]() 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为![]() ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
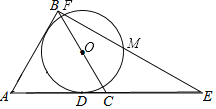
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com