
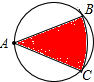
 如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为
如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为
| ||
| 6 |
| ||
| 6 |
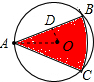 解:连接OA,作OD⊥AB于点D.
解:连接OA,作OD⊥AB于点D.| 1 |
| 2 |
| ||
| 2 |
| 3 |
60π×
| ||
| 180 |
| ||
| 3 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
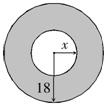 18、如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
18、如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:《28.3 用一元二次方程解决实际问题》2010年习题精选(四)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com