Question

 

（1）探究新知：

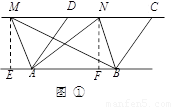
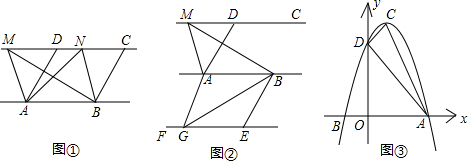
①如图，已知AD∥BC，AD＝BC，点M，N是直线CD上任意两点．

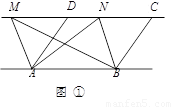
求证：△ABM与△ABN的面积相等． 

②如图，已知AD∥BE，AD＝BE，AB∥CD∥EF，点M是直线CD上任一点，点G是直线EF上任一点．试判断△ABM与△ABG的面积是否相等，并说明理由．  

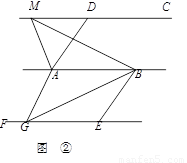
（2）结论应用：   

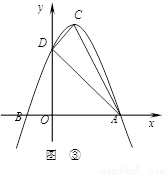
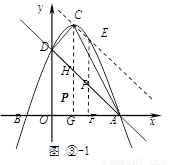
如图③，抛物线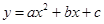的顶点为C（1，4），交x轴于点A（3，0），交y轴于点D．试探究在抛物线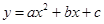上是否存在除点C以外的点E，使得△ADE与△ACD的面积相等？ 若存在，请求出此时点E的坐标，若不存在，请说明理由．

﹙友情提示：解答本问题过程中，可以直接使用“探究新知”中的结论．﹚    

 

Answer 1

【答案】

 

（1）①略

②相等．理由略

（2）存在，E点的坐标为E1（2，3）；；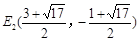

【解析】（本小题满分12分）

﹙1﹚①证明：分别过点M，N作 ME⊥AB，NF⊥AB，垂足分别为点E，F．

∵ AD∥BC，AD＝BC，

∴ 四边形ABCD为平行四边形．  

∴ AB∥CD．  

∴ ME= NF．   

∵S△ABM＝，S△ABN＝，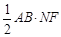

∴ S△ABM＝ S△ABN．   ……………………………………………………………………1分

②相等．理由如下：分别过点D，E作DH⊥AB，EK⊥AB，垂足分别为H，K．

则∠DHA=∠EKB=90°．

∵ AD∥BE，

∴ ∠DAH=∠EBK． 

∵ AD＝BE， 

∴ △DAH≌△EBK． 

∴ DH=EK．  ……………………………2分

∵ CD∥AB∥EF，   

∴S△ABM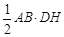＝，S△ABG＝， 

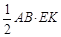∴  S△ABM＝ S△ABG.  …………………………………………………………………3分

﹙2﹚答：存在．  …………………………………………………………………………4分

解：因为抛物线的顶点坐标是C(1，4)，所以，可设抛物线的表达式为.

又因为抛物线经过点A(3，0)，将其坐标代入上式，得，解得.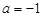

∴ 该抛物线的表达式为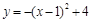，即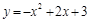．  ………………………5分

∴ D点坐标为（0，3）．

设直线AD的表达式为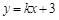，代入点A的坐标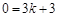，得，解得.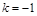

∴ 直线AD的表达式为．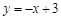  

过C点作CG⊥x轴，垂足为G，交AD于点H．则H点的纵坐标为．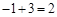

∴ CH＝CG－HG＝4－2＝2．  …………………………………………………………6分

设点E的横坐标为m，则点E的纵坐标为．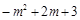   

过E点作EF⊥x轴，垂足为F，交AD于点P，则点P的纵坐标为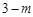，EF∥CG．

由﹙1﹚可知：若EP＝CH，则△ADE与△ADC的面积相等．

①若E点在直线AD的上方﹙如图③-1﹚，则P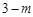F=，EF＝．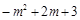

∴ EP＝EF－PF＝=．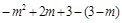 

∴ ． 

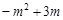解得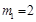，． ……………………………7分 

当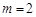时，PF=3－2＝1，EF=1+2＝3． 

∴ E点坐标为（2，3）．  

同理 当m=1时，E点坐标为（1，4），与C点重合．  ………………………………8分

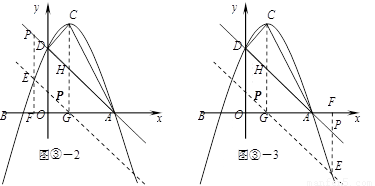
②若E点在直线AD的下方﹙如图③－2,③－3﹚，

则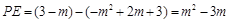．  ……………………………………………9分

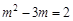∴．解得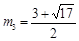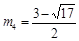，．   ………………………………10分

当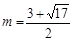时，E点的纵坐标为；   

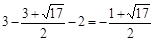当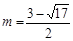时，E点的纵坐标为．  

∴ 在抛物线上存在除点C以外的点E，使得△ADE与△ACD的面积相等，E点的坐标为E1（2，3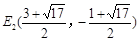）；；．  ………………12分

﹙其他解法可酌情处理﹚