
分析 (1)①根据题目中x、y的值可以求得x+y的值,从而可以解答本题;
②根据题目中x、y的值可以求得x+y和x-y的值,从而可以解答本题;
(2)先化简题目中的式子,再把a的值代入化简后的式子即可解答本题.
解答 解:(1)①∵x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,
∴x+y=$\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}$,x-y=$\sqrt{3}+1-(\sqrt{3}-1)=\sqrt{3}+1-\sqrt{3}+1=2$,
∴${x}^{2}+2xy+{y}^{2}=(x+y)^{2}=(2\sqrt{3})^{2}$=12;
②∵x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,
∴x+y=$\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}$,x-y=$\sqrt{3}+1-(\sqrt{3}-1)=\sqrt{3}+1-\sqrt{3}+1=2$,
∴x2-y2=(x+y)(x-y)=$2\sqrt{3}×2=4\sqrt{3}$;
(2)$\frac{2a}{{a}^{2}-4}$÷($\frac{{a}^{2}}{a-2}$-a)
=$\frac{2a}{(a+2)(a-2)}÷\frac{{a}^{2}-a(a-2)}{a-2}$
=$\frac{2a}{(a+2)(a-2)}×\frac{a-2}{2a}$
=$\frac{1}{a+2}$,
当a=$\sqrt{3}-2$时,原式=$\frac{1}{\sqrt{3}-2+2}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
点评 本题考查二次根式的化简求值、分式的化简求值,解答本题的关键是明确它们各自的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
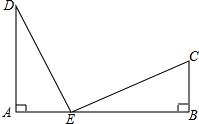 如图,铁路上A、B两点相距17千米,C、D为两村庄,DA⊥AB于A,CB⊥AB于B.已知DA=12km,CB=5km,现要在铁路AB上建一个土产品收购站E,使得C.D两村到E站的距离相等,则E站应建在离A站多少km处?
如图,铁路上A、B两点相距17千米,C、D为两村庄,DA⊥AB于A,CB⊥AB于B.已知DA=12km,CB=5km,现要在铁路AB上建一个土产品收购站E,使得C.D两村到E站的距离相等,则E站应建在离A站多少km处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
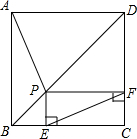 如图,在正方形ABCD中,点P是对角线BD上的一点(不与端点重合),过P作PE⊥BC于E,PF⊥CD于F,连接AP,EF.
如图,在正方形ABCD中,点P是对角线BD上的一点(不与端点重合),过P作PE⊥BC于E,PF⊥CD于F,连接AP,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
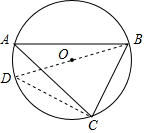 如图,⊙O是△ABC的外接圆,半径为R.已知BC=a,AC=b,AB=c.
如图,⊙O是△ABC的外接圆,半径为R.已知BC=a,AC=b,AB=c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
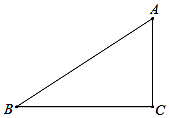 如图,在△ABC中,∠ACB=90°.
如图,在△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com