
【题目】(1)已知![]() 是关于
是关于![]() 的方程
的方程![]() 的解,求
的解,求![]() 的值.
的值.
(2)已知关于x的方程![]() 的解与方程
的解与方程![]() 的解互为倒数,求
的解互为倒数,求![]() 的值.
的值.
(3)小丽在解关于![]() 的方程
的方程![]() 时,出现了一个失误:“在将
时,出现了一个失误:“在将![]() 移到方程的左边时,忘记了变号.”结果她得到方程的解为
移到方程的左边时,忘记了变号.”结果她得到方程的解为![]() ,求
,求![]() 的值和原方程的解.
的值和原方程的解.
【答案】(1)7;(2)-1;(3)a=5,x=7.
【解析】试题分析:(1)把x=5代入方程ax-8=20+a得出方程5a-8=20+a,求出方程的解即可.
(2)求出两方程的解,根据解互为倒数列出关于a的方程,求出方程的解即可得到a2017的值.
(3)根据a的值没有改变,即可求出a的值,再代入正确的方程求出x的值即可.
试题解析:(1)把x=5代入方程ax﹣8=20+a,得5a-8=20+a,
解得a=7.
(2)由方程![]() 解得
解得![]() ,
,
因此由题意可知方程![]() 的解为
的解为![]() ,
,
代入可得![]() ,
,
解得![]() ,
,
∴![]() .
.
(3)根据题意知:小丽移项后所得方程为2x+ax=-21,
将x=-3代入这个方程可得:-6-3a=-21,
解得a=5.所以原方程为2x=5x-21,
解得x=7.
综上,a=5,原方程的解为x=7.


科目:初中数学 来源: 题型:
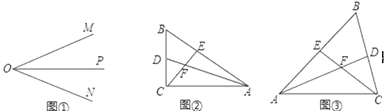
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求:
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC的三个顶点的横坐标乘以-1,纵坐标不变,则所得图形( )
A.与原图形关于x轴对称B.与原图形关于y轴对称
C.与原图形关于原点对称D.向y轴的负方向平移了一个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com