
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
【答案】(1)13,16;(2)3n﹣2;(3)2017.
【解析】
(1)第1个图形中,有3×1﹣2=1个正方形,第2个图形中有3×2﹣2=4个正方形,第3个图形中有3×3﹣2=7个正方形,第4个图形中有3×4﹣2=10个正方形,所以第5个图形中有3×5﹣2=13个正方形,第6个图形中有3×6﹣2=16个正方形;(2)第n个图形中有(3n﹣2)个正方形;(3)将n=673代入找出的规律中计算即可.
(1)按图示规律填写下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | 13 | 16 |
故答案为13,16;
(2))第1个图形中有1个正方形;
第2个图形中有3×2﹣2=4个正方形;
第3个图形中有3×3﹣2=7个正方形;
第4个图形中有3×4﹣2=10个正方形;
……
第n个图形有正方形(3n﹣2)个.
(3)第673个图中共有正方形的个数为3×673﹣2=2017.


科目:初中数学 来源: 题型:
【题目】如图,将一张等边三角形纸片沿各边中点剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;……,根据以上操作,若要得到100个小三角形,则需要操作的次数是( )

A. 25 B. 33 C. 34 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的单位长度为1,A、B两点表示的数是互为相反数;
(1)点A表示的数是 ,点B表示的数是
(2)数轴上一个动点P先向左移动2个单位长度,再向右移动5个单位到达点M,若点M表示的数是1,则点P所表示的数是
(3)(背景知识)数轴上,点A、B表示的数分别记为a、b,当点P在A、B之间,且到A、B的距离相等,即PA=PB,则点P表示的数可记为![]() .
.
若点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度向右运动,点P以1个单位长度/秒的速度从O点向右运动.当三点同时运动时,不妨设运动时间为t秒,(t>0)
①点P表示的数为 ;点A表示的数为 ;点B表示的数为 .(用含t的式子表示)
②当t为何值时,点A、点B、点P三点之间恰好有一个点到其他两个点的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)﹣7+13﹣6+20;
(2)3+(﹣2)﹣3×(﹣5)×0;
(3)16÷(﹣2)3﹣(﹣![]() )×(﹣4);
)×(﹣4);
(4)﹣36×(![]() );
);
(5)(2a2﹣1+2a)﹣(a﹣1+a2);
(6)8a+2b﹣2(5a﹣2b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49![]() ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下:
小明:原式=﹣![]() ×5=﹣
×5=﹣![]() =﹣249
=﹣249![]() ;
;
小军:原式=(49+![]() )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+![]() ×(﹣5)=﹣249
×(﹣5)=﹣249![]() ;
;
(1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19![]() ×(﹣8)
×(﹣8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某市8所学校抽取共1 000名学生进行800米跑达标抽样检测.结果显示该市达标学生人数超过半数,达标率达到52.5%.图l、图2反映的是本次抽样中的具体数据.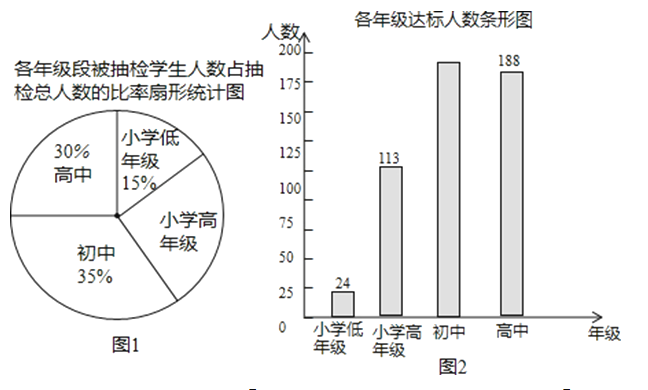
根据以上信息,下列判断:①小学高年级被抽检人数为200人;②小学、初中、高中学生中高中生800米跑达标率最大;③小学生800米跑达标率低于33%;④高中生800米跑达标率超过70%.其中判断正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为![]() .
.
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com