
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,![]() ),(5,
),(5,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(﹣2,1),(3,![]() )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;
(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
【答案】(1)(3,![]() )是“共生有理数对”;(2)是(3)(4,
)是“共生有理数对”;(2)是(3)(4,![]() )或(6,
)或(6,![]() )等;(4)a=﹣2
)等;(4)a=﹣2
【解析】
(1)计算后,根据“共生有理数对”的定义判定即可;(2)根据(m,n)是“共生有理数对”可得m-n=mn+1,根据根据“共生有理数对”的定义即可证明;(3)根据“共生有理数对”的定义写出符合条件的数对即可(注意:不能与题目中已有的“共生有理数对”重复);(4)根据“共生有理数对”的定义可得a-(-3)=-3a+1,由此即可求得a值.
(1)-2-1=-3,(-2) ×1+1=-1,-3≠-1,故(-2,1)不是共生有理数对;3-![]() =
=![]() ,3×
,3×![]() +1=
+1=![]() ,故(3,
,故(3,![]() )是共生有理数对;
)是共生有理数对;
故答案为:(3,![]() );
);
(2)是.
理由: -n-(-m)=-n+m,-n×(-m)+1=mn+1 ,
∵(m,n)是“共生有理数对”
∴m-n=mn+1,
∴-n+m=mn+1,
∴(-n,-m)是“共生有理数对”;
(3)(4,![]() )或6,
)或6,![]() )等(答案不唯一,只要不和题中重复即可);
)等(答案不唯一,只要不和题中重复即可);
(4)由题意可知,a-(-3)=-3a+1,
解得a=![]() .
.


科目:初中数学 来源: 题型:
【题目】函数 y=![]() (a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的集合内:
100,﹣0.82,﹣30![]() ,3.14,﹣2,0,﹣2011,﹣3.1
,3.14,﹣2,0,﹣2011,﹣3.1![]() ,
,![]() ,﹣
,﹣![]() ,2.010010001…,
,2.010010001…,
正分数集合:{ …}
整数集合:{ …}
负有理数集合:{ …}
非正整数集合;{ …}
无理数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.请根据信息解答下列问题:
(1)图1中淘米水浇花所在的扇形的圆心角度数为__________________;
(2)补全图2;
(3)求120名同学家庭月人均用水量的中位数和众数;
(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?

图1
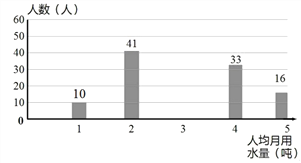
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)OD与OE的位置关系是______;(2)∠EOC的余角是_______ .
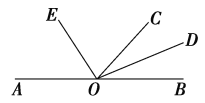
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
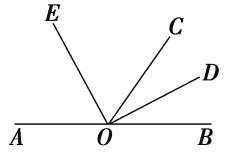
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( ) 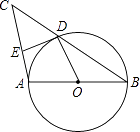
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com