
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

【答案】(1) 25°;(2) ∠E=β-α
【解析】
(1)由∠B=35°,∠ACB=85°,根据三角形内角和等于180°,可得∠BAC的度数,因为AD平分∠BAC,从而可得∠DAC的度数,进而求得∠ADC的度数,由PE⊥AD,可得∠DPE的度数,从而求得∠E的度数.
(2)根据第一问的推导,可以用含α、β的代数式表示∠E.
(1)∵∠B=35°,∠ACB=85°,∴∠BAC=180°-∠B-∠ACB=60°.
∵AD平分∠BAC,∴∠DAC=∠BAD=30°.
∴∠ADC=∠B+∠BAD=65°.
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADC=25°.
(2)∵∠B=α,∠ACB=β,∴∠BAC=180°-α-β.
∵AD平分∠BAC,∴∠DAC=∠BAD=(180°-α-β).
∴∠ADE=∠B+∠BAD=90°+α-β,
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADE=β-α.


科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的形统计图和不完整的条形统计图:
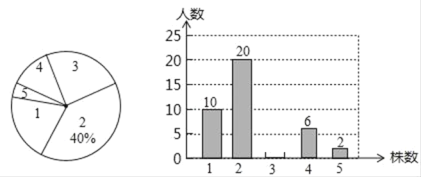
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)该班同学植树株数的中位数是 ;
(3)求该班同学平均植树的株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月12日,安庆“筑梦号”自动驾驶公开试乘体验正式启动,让安庆成为全国率先开通自动驾驶的城市,智能、绿色出行的时代即将到来.普通燃油车从A地到B地,所需油费108元,而自动驾驶的纯电动车所需电费27元,已知每行驶l千米,普通燃油汽车所需的油费比自动的纯电动汽车所需的电费多0.54元,求自动驾驶的纯电动汽车每行驶1千米所需的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图).

(1)当点E与点B重合时,点F恰好与点C重合(如图),则PC的长为 ;
(2)将直角尺从如图中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径(线段)长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
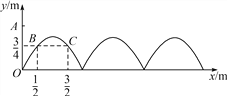
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用y=ax2+bx(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10 m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k。这样的三角形称为比高三角形,其中k叫做比高系数。根据规定解答下列问题:
(1)周长为13的比高三角形的比高系数k= ;
(2)比高三角形△ABC三边与它的比高系数k之间满足BC-AC=AC-AB=k2,求△ABC的周长的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】打折前,买6件A商品和3件B商品用了108元,买5件A商品和1件B商品用了84元,打折后买5件A商品和5件B商品用了80元。问打折后买5件A商品和5件B商品比不打折少花多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com