
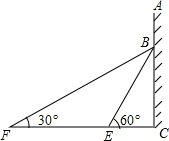
 如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.
如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.分析 (1)设CE=x,根据勾股定理及直角三角形的性质表示出BC、BE长,利用等角对等边易得BE=FE,那么就求得了CE长,进而求得BC长.
(2)根据(1)的结果可求得CF=60,根据已知求得小明的速度,然后根据速度、时间、路程的关系即可求得.
解答 解:设CE=x
在Rt△BCE中,∠BCE=90°,∠BEC=60°
∴∠EBC=30°.
由勾股定理得:BE=2x,BC=$\sqrt{3}$x,
∵∠BEC=60°,∠F=30°
∴∠FBE=30°,
∴∠FBE=30°,
∴∠FBE=∠F,
∴BE=EF=2x,
∴EF=40,
∴2x=40,
∴x=20,
∴BC=20$\sqrt{3}$.
答:建筑物BC的长为34.6m.
(2)∵CE=20,EF=40,
∴CF=60,
小明的速度为40÷80=0.5(米/秒),
小明从点F到点C所用的时间为60÷0.5=120秒
答:小明从点F到点C所用的时间为120秒.
点评 本题考查了解直角三角形的应用-仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点D为函数y=$\frac{18}{x}$(x>0)上 的一点,四边形ABCD是直角梯形(点B在坐标原点处),AD∥BC,∠B=90°,A(0,3),C(4,0),点P从A出发,以4个单位/秒的速度沿直线AD向右运动,点Q从点C同时出发,以2个单位/秒的速度沿直线CB向左运动.
如图,在平面直角坐标系中,已知点D为函数y=$\frac{18}{x}$(x>0)上 的一点,四边形ABCD是直角梯形(点B在坐标原点处),AD∥BC,∠B=90°,A(0,3),C(4,0),点P从A出发,以4个单位/秒的速度沿直线AD向右运动,点Q从点C同时出发,以2个单位/秒的速度沿直线CB向左运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填写下题的步骤和依据.如图所示,已知△ABC中,FG∥BE,∠2=∠3,则∠EDB+∠DBC=180°?为什么?
填写下题的步骤和依据.如图所示,已知△ABC中,FG∥BE,∠2=∠3,则∠EDB+∠DBC=180°?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com