
| 1 |
| x1+x2+x1x2 |
| 1 |
| p |
| 1 |
| p |
| 2 |
| p |
| p |
| 2 |
科目:初中数学 来源:新教材新学案数学九年级上册 题型:044
判断下列关于x的方程是不是一元二次方程:
(1)x2-5x=0;
(2)x2-2xy-3=0;
(3)![]() ;
;
(4)![]() ;
;
(5)2x(x-3)=2x2+1;
(6)![]() ;
;
(7)px2+qx+m=0;
(8)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
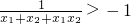 ,求实数p的取值范围.
,求实数p的取值范围. ,x1•x2=-
,x1•x2=- ,∴x1+x2+x1•x2=-
,∴x1+x2+x1•x2=-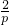 ,∴-
,∴- >-1,解得p<2,∴实数的取值范围是p<2,判断以上解法是否正确?若不正确,请你给出一个你认为正确的解答过程.
>-1,解得p<2,∴实数的取值范围是p<2,判断以上解法是否正确?若不正确,请你给出一个你认为正确的解答过程.查看答案和解析>>
科目:初中数学 来源:奉贤区二模 题型:解答题
| 1 |
| x1+x2+x1x2 |
| 1 |
| p |
| 1 |
| p |
| 2 |
| p |
| p |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2004年上海市奉贤区中考数学二模试卷(解析版) 题型:解答题
 ,求实数p的取值范围.
,求实数p的取值范围. ,x1•x2=-
,x1•x2=- ,∴x1+x2+x1•x2=-
,∴x1+x2+x1•x2=- ,∴-
,∴- >-1,解得p<2,∴实数的取值范围是p<2,判断以上解法是否正确?若不正确,请你给出一个你认为正确的解答过程.
>-1,解得p<2,∴实数的取值范围是p<2,判断以上解法是否正确?若不正确,请你给出一个你认为正确的解答过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com