
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE. 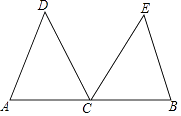
(1)求证:△ACD≌△BCE;
(2)若∠D=53°,求∠B的度数.
【答案】
(1)证明:∵CD平分∠ACE,
∴∠ACD=∠DCE,
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠ACD=∠BCE,
∵C是线段AB的中点,
∴AC=BC.
在△ACD与△BCE中 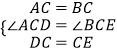 ,
,
∴△ACD≌△BCE
(2)解:∵∠ACD=∠DCE=∠BCE= ![]() 180°=60°,
180°=60°,
∵△ACD≌△BCE,
∴∠E=∠D=53°,
∴∠B=180°﹣60°﹣53°=67°
【解析】(1)根据角平分线的定义得到∠ACD=∠BCE,由C是线段AB的中点,得到AC=BC.根据全等三角形的判定定理即可得到结论;(2)根据平角的定义得到∠ACD=∠DCE=∠BCE=60°,根据全等三角形的性质得到∠E=∠D=53°,根据三角形的内角和即可得到结论.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
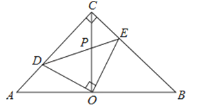
【题目】如图,在等腰直角△ABC中,∠ACB=90°,点O为斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:
①图中全等三角形有三对;②△ABC的面积等于四边形CDOE面积的![]() 倍;③DE2+2CDCE=2OA2;④AD2+BE2=2OPOC.正确的有( )个.
倍;③DE2+2CDCE=2OA2;④AD2+BE2=2OPOC.正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.
(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之积能被2整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c过点B(3,0),C(0,﹣3),D为抛物线的顶点.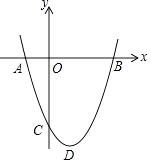
(1)求抛物线的解析式以及顶点坐标;
(2)点C关于抛物线y=x2﹣bx+c对称轴的对称点为E点,连接BC,BE,求∠CBE的正切值;
(3)在(2)的条件下,点M是抛物线对称轴上且在CE上方的一点,是否存在点M使△DMB和△BCE相似?若存在,求点M坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,动点Q从点A出发,沿着AB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着对角线BD方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PB长为半径的⊙P与BD、AB的另一个交点分别为E、F,连结EF、QE. 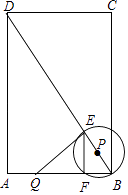
(1)填空:FB=(用t的代数式表示);
(2)当t为何值时,点Q与点F相遇?
(3)当线段QE与⊙P有两个公共点时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学决定在八年级阳光体育“大课间”活动中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: 
(1)在这项调查中,共调查了多少名学生?
(2)将两个统计图补充完整;
(3)若调查到喜欢“立定跳远”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(a,b)、B(1,4)(a>1)是反比例函数y= ![]() (x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”)
(x>0)图象上两点,过A、B分别作x轴、y轴的垂线,垂足分别为C、D、E、F,AE、BD交于点G.则四边形ACDG的面积随着a的增大而 . (填“减小”、“不变”或“增大”) 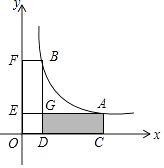
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com