
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )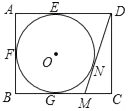
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】连接OE,OF,ON,OG,
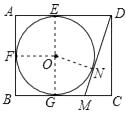
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5﹣2﹣MN=3﹣MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3﹣NM)2+42,
∴NM= ![]() ,
,
∴DM=3 ![]() =
= ![]() ,
,
故答案为:A.
易得四边形ABMD外切于⊙O,由切线的性质易得∠AEO=∠AFO=∠OFB=∠BGO=90°,四边形AFOE,FBGO是正方形;AF=BF=AE=BG=2,DE=3。在R t△CDM中,利用MN表示三边,再利用勾股定理可得MN的值,最后可得DM的值。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
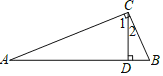
【题目】如图,直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)找出图中相等的锐角,并说明理由.
(2)求出点![]() 到直线
到直线![]() 的距离以及点
的距离以及点![]() 到直线
到直线![]() 的距离.
的距离.
解:(1)![]() (已知),
(已知),
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
同理可证,
![]() .
.
(2)点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
![]() 到直线
到直线![]() 的距离为线段 的长度.
的距离为线段 的长度.
![]()
![]()
![]()
![]() (填线段名称).
(填线段名称).
![]() ,
,![]() ,
,![]() ,代入上式,解得
,代入上式,解得
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
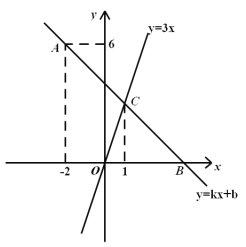
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像经过点
的图像经过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() ,与正比例函数
,与正比例函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]()
![]() 的值;
的值;
(2)若点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人. 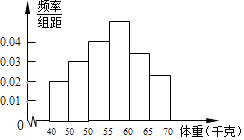
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com