
如图,△ABC内接于⊙O,AB是⊙O的直径,C是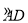 的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD
的中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD

(1)求证:∠ACH=∠CBD;
(2)求证:P是线段AQ的中点;
(3)若⊙O 的半径为5,BH=8,求CE的长.
(1)证明见解析;(2)证明见解析;(3)8.
【解析】
试题分析:(1)根据垂径定理得出AB垂直平分CE,推出H为CE中点,弧AC=弧AE,根据圆周角定理推出即可.
(2)根据圆周角定理求出∠ACH=∠CAD,推出AP=CP,求出∠PCQ=∠CQP,推出PC=PQ,即可得出答案.
(3)连接OC,根据勾股定理求出CH,根据垂径定理求出即可.
试题解析:(1)证明:∵AB是⊙O的直径,CE⊥AB,
∴AB垂直平分CE,
即H为CE中点,弧AC=弧AE
又∵C是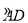 的中点,
的中点,
∴弧AC=弧CD
∴弧AC=弧CD=弧AE
∴∠ACH=∠CBD;
(2)由(1)知,∠ACH=∠CBD,
又∵∠CAD=∠CBD
∴∠ACH=∠CAD,
∴AP=CP
又∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴∠PCQ=90°﹣∠ACH,∠PQC=∠BQD=90°﹣∠CBD,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,
即P是线段AQ的中点;
(3)【解析】
连接OC,
∵BH=8,OB=OC=5,
∴OH=3
∴由勾股定理得:CH=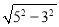 =4
=4
由(1)知:CH=EH=4,
∴CE=8.
考点:1.三角形的外接圆与外心;2.勾股定理;垂径定理;3.圆心角、弧、弦的关系.


科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分7分)已知关于 的方程
的方程 .
.
(1)试说明:无论 取什么实数值,方程总有实数根;
取什么实数值,方程总有实数根;
(2)若等腰 的一边长
的一边长 为1,另两边长
为1,另两边长 、
、 恰好是这个方程的两个实数根,求
恰好是这个方程的两个实数根,求 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:解答题
(本题满分12分)如图,已知抛物线 经过点
经过点 、
、 ,交
,交 轴于点
轴于点 .
.

(1)求此抛物线的解析式;
(2)抛物线第一象限上有一动点 ,过点
,过点 作
作 轴,垂足为
轴,垂足为 ,请求出
,请求出 的最大值,及此时点
的最大值,及此时点 坐标;
坐标;
(3)抛物线顶点为 ,
, 轴于
轴于 点,一块三角板直角顶点
点,一块三角板直角顶点 在线段
在线段 上滑动,且一直角边过
上滑动,且一直角边过 点,另一直角边与
点,另一直角边与 轴交于
轴交于 ,请求出实数
,请求出实数 的变化范围,并说明理由.
的变化范围,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:填空题
如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率 飞镖落在白色区域的概率.(填“ ”“
”“ ”“
”“ ”)
”)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:解答题
在直径是52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度CD为16cm,求油面宽度AB的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省容城镇三闾学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
抛物线 的顶点坐标是( )
的顶点坐标是( )
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com