
【题目】发现与探索。
(1)根据小明的解答将下列各式因式分解

① a2-12a+20;②(a-1)2-8(a-1)+7;③ a2-6ab+5b2
(2)根据小丽的思考解决下列问题:

①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
【答案】(1)①(a-10)(a-2);②(a-7)(a-3);③(a-5b)(a-b);(2)①说明见解析;②﹣a2+12a-8.的最大值为28.
【解析】(1)①把所给的多项式加上36后再减去36,类比小明的解法,前三项利用完全平方公式因式分解后,再利用平方差公式因式分解即可;②把所给的多项式加上16后再减去16,类比小明的解法,前三项利用完全平方公式因式分解后,再利用平方差公式因式分解即可;③把所给的多项式加上9b2后再减去9b2,类比小明的解法,前三项利用完全平方公式因式分解后,再利用平方差公式因式分解即可;(2)①把所给的多项式化为(a-6)2-16后,根据非负数的性质可得(a-6)2≥0,当x=6时,所给多项式的最小值为-16;②根据非负数的性质可得无论a取何值-(a+1)2都小于等于0,再加上8,即可得代数式-(a+1)2+8小于等于8,所以-(a+1)2+8的最大值为8;把所给的多项式化为﹣(a-6)2+28后,类比上面的解题方法解答即可.
(1)①a2-12a+20
原式=a2-12a+36-36+20
=(a-6)2-42
=(a-10)(a-2)
②(a-1)2-8(a-1)+12
原式=(a-1)2-8(a-1)+16-16+12
=(a-5)2-22
=(a-7)(a-3)
③a2-6ab+5b2
原式=a2-6ab+9b2-9b2+5b2
=(a-3b)2-4b2
=(a-5b)(a-b)
(2)根据小明的发现结合小丽的思考解决下列问题.
①说明:代数式a2-12a+20的最小值为﹣16.
a2-12a+20
原式=a2-12a+36-36+20
=(a-6)2-16
无论a取何值(a-6)2都大于等于0,再加上﹣16,
则代数式(a-6)2-16大于等于-16,
则a2-12a+20的最小值为-16
②无论a取何值-(a+1)2都小于等于0,再加上8,
则代数式-(a+1)2+8小于等于8,
则-(a+1)2+8的最大值为8
﹣a2+12a-8.
原式=﹣(a2-12a+8)
=﹣(a2-12a+36-36+8)
=﹣(a-6)2+36-8
=﹣(a-6)2+28
无论a取何值﹣(a-6)2都小于等于0,再加上28,
则代数式﹣(a-6)2+28小于等于28,
则﹣a2+12a-8的最大值为28.


科目:初中数学 来源: 题型:
【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).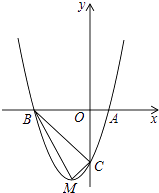
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司以每吨![]() 元的价格收购了
元的价格收购了![]() 吨某种药材,若直接在市场上销售,每吨的售价是
吨某种药材,若直接在市场上销售,每吨的售价是![]() 元.该公司决定加工后再出售,相关信息如下表所示:
元.该公司决定加工后再出售,相关信息如下表所示:
工艺 | 每天可加工药材的吨数 | 成品率 | 成品售价 (元/吨) |
粗加工 | 14 | 80% | 6000 |
精加工 | 6 | 60% | 11000 |
(注:①成品率80%指加工100吨原料能得到80吨可销售药材;②加工后的废品不产生效益.)
受市场影响,该公司必须在![]() 天内将这批药材加工完毕.
天内将这批药材加工完毕.
(1)若全部粗加工,可获利_______________________元;
(2)若尽可能多的精加工,剩余的直接在市场上销售,可获利_____________元;
(3)若部分粗加工,部分精加工,恰好![]() 天完成,求可获利多少元?
天完成,求可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,三角形ABC是等边三角形,D是BC边上的一点,三角形ABD经过旋转后到达三角形ACE的位置.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋转后,点M到了什么位置?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).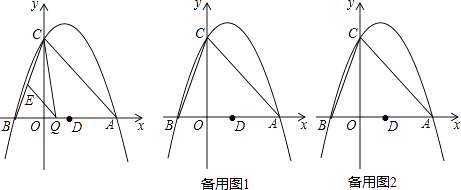
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°,BC=2,按照如下步骤作图:①分别以点A,B为圆心,大于线段AB长度的一半为半径画弧,两弧分别相交于点M,N;②作直线MN分别交AB,AC于点D,E,连结BE,则BE的长是( ) 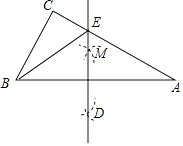
A.![]()
B.3
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com