
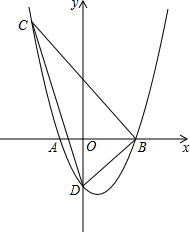
 如图,抛物线经过A(-1,0),B(3,0),C(-2,5)三点,与y轴交于点D.
如图,抛物线经过A(-1,0),B(3,0),C(-2,5)三点,与y轴交于点D.分析 (1)令y=a(x+1)(x-3),根据待定系数法可求抛物线的解析式;
(2)先根据抛物线的解析式得到D(0,-3),再结合已知条件根据三角函数即可求解;
(3)①先根据∠CBD=90°,得到CD为⊙M的直径,根据中点坐标公式可得M(-1,1),OE=5,作MH⊥DF,垂足H,得到DF=BE=8,再根据三角形面积公式即可求解;
②分两种情况:当点P在x轴上方时;当点P在x轴下方时;根据相似三角形的判定和性质进行讨论即可求得点P的坐标.
解答 解:(1)令y=a(x+1)(x-3),
代入(-2,5),得a(-2+1)(-2-3)=5,
解得a=1,
故抛物线的解析式为y=x2-2x-3;
(2)D(0,-3),
∵B(3,0),
∴OB=OD,
∴∠OBD=45°,$BD=3\sqrt{2}$
∵C(-2,5),
∴$tan∠CBO=\frac{5}{3-(-2)}=1$,
∴∠CBO=45°,$BC=5\sqrt{2}$,
∴∠CBD=90°,
∴$tan∠BCD=\frac{{3\sqrt{2}}}{{5\sqrt{2}}}=\frac{3}{5}$;
(3)①∵∠CBD=90°,
∴CD为⊙M的直径, ∵C(-2,5),D(0,-3),
∵C(-2,5),D(0,-3),
∴M(-1,1),
∵A(-1,0),
∴AM⊥BE,
∴BE=2AB=8,
∴E(-5,0),
∴OE=5,
如图1,作MH⊥DF,垂足H,
∵MH⊥MA,
∴DF=BE=8,
∴${S_{△DEF}}=\frac{8×5}{2}=20$;  ②如图2,当点P在x轴上方时,设DP交x轴于点N.
②如图2,当点P在x轴上方时,设DP交x轴于点N.
∵∠BDP=∠BED,∠DBN=∠EBD,
∴△BDN∽△BED,
∴BD2=BN•BE,
∴$BN=\frac{9}{4}$,
∴N($\frac{3}{4}$,0),
∴直线DN的解析式y=4x-3,
由题意得x2-2x-3=4x-3,
解得x1=0,x2=6,
∴P(6,21),
如图3,当点P在x轴下方时,设DP交x轴于点G,CD交x轴于点I. 可求得直线CD的解析式y=-4x-3,
可求得直线CD的解析式y=-4x-3,
∴I($-\frac{3}{4}$,0),
∵∠BDP=∠BED=∠BCD,
∴∠CDP=∠BDP+∠CDB=∠BCD+∠CDB=90°,
∵OD⊥AG,
∴∠IDO=∠OGD,
∵∠IOD=∠DOG=90°,
∴△IOD∽△DOG,
∴OD2=OG•OI,
∴OG=12,
∴G(12,0),
∴直线DG的解析式$y=\frac{1}{4}x-3$,
由题意得${x^2}-2x-3=\frac{1}{4}x-3$,
解得${x_1}=0,{x_2}=\frac{9}{4}$,
∴P($\frac{9}{4}$,$-\frac{39}{16}$)
∴点P的坐标为(6,21)或($\frac{9}{4}$,$-\frac{39}{16}$).
点评 考查了二次函数综合题,涉及的知识点有:待定系数法可求抛物线的解析式,坐标轴上点的坐标特征,三角函数,中点坐标公式,三角形面积,相似三角形的判定和性质,分类思想的运用,综合性较强,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
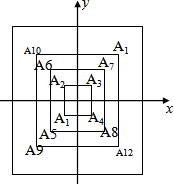 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A1,A2,A3,A4,…表示,则顶点A2013的坐标是(-504,-504).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 A1,A2,A3,A4,…表示,则顶点A2013的坐标是(-504,-504).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.
已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
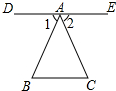 如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.
如图,有下列三个条件:①DE∥BC;②∠1=∠2;③∠B=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
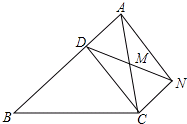 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
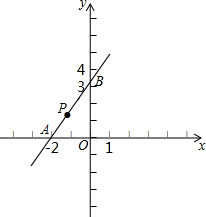 如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)
如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com