
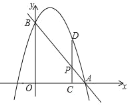
【题目】如图,已知直线y=﹣x+4分别交x轴、y轴于点A、B,抛物线过y=ax2+bx+c经过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
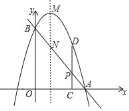
(1)若抛物线的解析式为y=﹣![]() x2+x+4,设其顶点为M,其对称轴交AB于点N.
x2+x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为2时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形是直角三角形?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
【答案】(1)① M(1,![]() ),N(1,3); ②见解析;(2)见解析.
),N(1,3); ②见解析;(2)见解析.
【解析】
(1)①把二次函数表达式化为顶点式表达式,即可求解;
②不存在.理由如下:设点P 的坐标为(m,-m+4),则D(m,-![]() m2+m+4),PD=-
m2+m+4),PD=-![]() m2+m+4-(-m+4)=-
m2+m+4-(-m+4)=-![]() m2+2m,当四边形MNPD为平行四边形,则:
m2+2m,当四边形MNPD为平行四边形,则:![]() m2+2m=
m2+2m=![]() ,解得:m=1,则:点P(3,1),由N(1,3),则:PN=
,解得:m=1,则:点P(3,1),由N(1,3),则:PN=![]() ≠MN,即可求解;
≠MN,即可求解;
(2)分∠BDP=90°或∠PBD=90°两种情况,求解即可.
解:(1)①y=﹣![]() x2+x+4=﹣
x2+x+4=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∴顶点M的坐标为(1,![]() ),
),
当x=1时,y=﹣1+4=3,
∴点N的坐标为(1,3);
②不存在.理由如下:
MN=![]() ﹣3=
﹣3=![]() ,
,
设点P 的坐标为(m,﹣m+4),则D(m,﹣![]() m2+m+4),
m2+m+4),
PD=﹣![]() m2+m+4﹣(﹣m+4)=﹣
m2+m+4﹣(﹣m+4)=﹣![]() m2+2m,
m2+2m,
∵PD∥MN.
∴当PD=MN时,四边形MNPD为平行四边形,
即﹣![]() m2+2m=
m2+2m=![]() ,解得:m=1或3(m=1舍去),
,解得:m=1或3(m=1舍去),
∴点P(3,1),由N(1,3),
∴PN=![]() ≠MN,
≠MN,
∴平行四边形MNPD不是菱形,
即:不存在点P,使四边形MNPD为菱形;
(2)①当∠BDP=90°时,点P(2,2),则四边形BOCD为矩形,
∴D(2,4),又A(4,0),B(0,4),
∴抛物线的表达式为:y=﹣![]() x2+x+4;
x2+x+4;
②当∠PBD=90°时,△PBD为等腰直角三角形,
则PD=2xP=4,
∴D(2,6),又A(4,0),B(0,4),
把A、B、D坐标代入二次函数表达式得: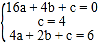 ,解得:
,解得: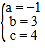 ,
,
故:二次函数表达式为:y=﹣x2+3x+4.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】周六上午,小红到少年宫参加9点整开始的舞蹈表演.小红8点整从家步行出发,计划提前20min到达.小红步行了900m后发现一件道具忘在家里桌上,她立刻以原来速度的1.5倍沿原路返回,8点25分到达家中.
(1)求小红原来的步行速度.
(2)小红为确保不迟于8点40分到达少年宫,她拿到道具后,以12km/h的速度匀速骑自行车立即按原线路赶往少年宫.问小红在家最多只能耽搁多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B②当x=1时,四边形ABC1D1是菱形 ③当x=2时,△BDD1为等边三角形 ④s=![]() (x﹣2)2(0<x<2),其中正确的有( )
(x﹣2)2(0<x<2),其中正确的有( )
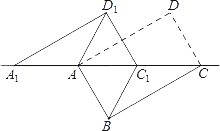
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
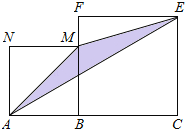
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个不透明的袋子中装有7个只有颜色不同的球,其中2个白球,5个红球.
(1)求从袋中随机摸出一个球是红球的概率.
(2)从袋中随机摸出一个球,记录颜色后放回,摇匀,再随机摸出一个球,求两次摸出的球恰好颜色不同的概率.
(3)若从袋中取出若干个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为![]() ,求袋中有几个红球被换成了黄球.
,求袋中有几个红球被换成了黄球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)求证:四边形 BFCE 是平行四边形.
(2)若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com