
【题目】已知抛物线y=ax2+bx+c.
(Ⅰ)若抛物线的顶点为A(﹣2,﹣4),抛物线经过点B(﹣4,0)
①求该抛物线的解析式;
②连接AB,把AB所在直线沿y轴向上平移,使它经过原点O,得到直线l,点P是直线l上一动点.
设以点A,B,O,P为顶点的四边形的面积为S,点P的横坐标为x,当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,求x的取值范围;
时,求x的取值范围;
(Ⅱ)若a>0,c>1,当x=c时,y=0,当0<x<c时,y>0,试比较ac与l的大小,并说明理由.
【答案】(Ⅰ)①y=x2+4x②当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,x的取值范围为是
时,x的取值范围为是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤
≤x≤![]() (Ⅱ)ac≤1
(Ⅱ)ac≤1
【解析】
(I)①由抛物线的顶点为A(-2,-4),可设抛物线的解析式为y=a(x+2)2-4,代入点B的坐标即可求出a值,此问得解,②根据点A、B的坐标利用待定系数法可求出直线AB的解析式,进而可求出直线l的解析式,分点P在第二象限及点P在第四象限两种情况考虑:当点P在第二象限时,x<0,通过分割图形求面积法结合4+6![]() ≤S≤6+8
≤S≤6+8![]() ,即可求出x的取值范围,当点P在第四象限时,x>0,通过分割图形求面积法结合4+6≤S≤6+8
,即可求出x的取值范围,当点P在第四象限时,x>0,通过分割图形求面积法结合4+6≤S≤6+8![]() ,即可求出x的取值范围,综上即可得出结论,(2)由当x=c时y=0,可得出b=-ac-1,由当0<x<c时y>0,可得出抛物线的对称轴x=
,即可求出x的取值范围,综上即可得出结论,(2)由当x=c时y=0,可得出b=-ac-1,由当0<x<c时y>0,可得出抛物线的对称轴x=![]() ≥c,进而可得出b≤-2ac,结合b=-ac-1即可得出ac≤1.
≥c,进而可得出b≤-2ac,结合b=-ac-1即可得出ac≤1.
(I)①设抛物线的解析式为y=a(x+2)2﹣4,
∵抛物线经过点B(﹣4,0),
∴0=a(﹣4+2)2﹣4,
解得:a=1,
∴该抛物线的解析式为y=(x+2)2﹣4=x2+4x.
②设直线AB的解析式为y=kx+m(k≠0),
将A(﹣2,﹣4)、B(﹣4,0)代入y=kx+m,
得:![]() ,解得:
,解得:![]() ,
,
∴直线AB的解析式为y=﹣2x﹣8.
∵直线l与AB平行,且过原点,
∴直线l的解析式为y=﹣2x.
当点P在第二象限时,x<0,如图所示.
S△POB=![]() ×4×(﹣2x)=﹣4x,S△AOB=
×4×(﹣2x)=﹣4x,S△AOB=![]() ×4×4=8,
×4×4=8,
∴S=S△POB+S△AOB=﹣4x+8(x<0).
∵4+6![]() ≤S≤6+8
≤S≤6+8![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ≤x≤
≤x≤![]() ,
,
∴x的取值范围是![]() ≤x≤
≤x≤![]() .
.
当点P′在第四象限时,x>0,
过点A作AE⊥x轴,垂足为点E,过点P′作P′F⊥x轴,垂足为点F,则
S四边形AEOP′=S梯形AEFP′﹣S△OFP′=![]() (x+2)﹣
(x+2)﹣![]() x(2x)=4x+4.
x(2x)=4x+4.
∵S△ABE=![]() ×2×4=4,
×2×4=4,
∴S=S四边形AEOP′+S△ABE=4x+8(x>0).
∵4+6![]() ≤S≤6+8
≤S≤6+8![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ≤x≤
≤x≤![]() ,
,
∴x的取值范围为![]() ≤x≤
≤x≤![]() .
.
综上所述:当4+6![]() ≤S≤6+8
≤S≤6+8![]() 时,x的取值范围为是
时,x的取值范围为是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤
≤x≤![]() .
.
(II)ac≤1,理由如下:
∵当x=c时,y=0,
∴ac2+bc+c=0,
∵c>1,
∴ac+b+1=0,b=﹣ac﹣1.
由x=c时,y=0,可知抛物线与x轴的一个交点为(c,0).
把x=0代入y=ax2+bx+c,得y=c,
∴抛物线与y轴的交点为(0,c).
∵a>0,
∴抛物线开口向上.
∵当0<x<c时,y>0,
∴抛物线的对称轴x=﹣![]() ≥c,
≥c,
∴b≤﹣2ac.
∵b=﹣ac﹣1,
∴﹣ac﹣1≤﹣2ac,
∴ac≤1.


科目:初中数学 来源: 题型:
【题目】有一家糖果加工厂,它们要对一款奶糖进行包装,要求每袋净含量为100g.现使用甲、乙两种包装机同时包装100g的糖果,从中各抽出10袋,测得实际质量(g)如下:
甲:101,102,99,100,98,103,100,98,100,99
乙:100,101,100,98,101,97,100,98,103,102
(1)分别计算两组数据的平均数、众数、中位数;
(2)要想包装机包装奶糖质量比较稳定,你认为选择哪种包装机比较适合?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了![]() ,
,![]() 两种型号的空气净化器,已知一台
两种型号的空气净化器,已知一台![]() 型空气净化器的进价比一台
型空气净化器的进价比一台![]() 型空气净化器的进价多300元,用7500元购进
型空气净化器的进价多300元,用7500元购进![]() 型空气净化器和用6000元购进
型空气净化器和用6000元购进![]() 型空气净化器的台数相同.
型空气净化器的台数相同.
(1)求一台![]() 型空气净化器和一台
型空气净化器和一台![]() 型空气净化器的进价各为多少元?
型空气净化器的进价各为多少元?
(2)在销售过程中,![]() 型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划
型空气净化器因为净化能力强,噪声小而更受消费者的欢迎.商社电器计划![]() 型净化器的进货量不少于20台且是
型净化器的进货量不少于20台且是![]() 型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
型净化器进货量的三倍,在总进货款不超过5万元的前提下,试问有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F是AC上的动点,BD=DF
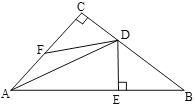
(1)求证:BE=FC;
(2)若∠B=30°,DC=2,此时![]() ,求△ACB的面积.
,求△ACB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
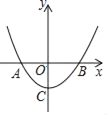
【题目】如图,二次函数y=x2﹣m2(m>0且为常数)的图象与x轴交于点A、B(A在B左侧),与y轴交于C.
(1)求A,B,C三点的坐标(用含m的式子表示);
(2)若∠ACB=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
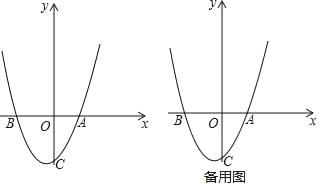
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0),B(﹣5,0),C(0,﹣5)三点,O为坐标原点.
(1)求此抛物线的解析式;
(2)把抛物线y=ax2+bx+c(a≠0)向上平移![]() 个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
个单位长度,再向左平移n(n>0)个单位长度得到新抛物线,若新抛物线的顶点M在△ABC内,求n的取值范围;
(3)设点P在y轴上,且满足∠OPA+∠OCA=∠CBA,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
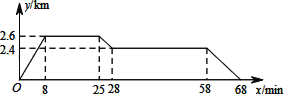
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
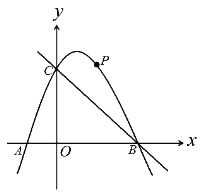
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.
的图象与x轴交于A、B两点, 与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0))。点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形![]() ,那么是否存在点P,使四边形
,那么是否存在点P,使四边形![]() 为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,使△BPC的面积最大,求出点P的坐标和△BPC的面积最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com