
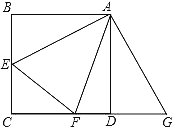
【题目】如图,正方形ABCD中,E、F分别是边BC,CD上一点,∠EAF=45°.将△ABE绕着点A逆时针旋转90°得到△ADG,连接EF,求证EF=FG.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点A、B,且过点C(4,3).
轴相交于点A、B,且过点C(4,3).
(1)求![]() 的值和该抛物线顶点P的坐标;
的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
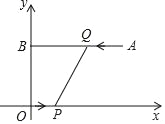
【题目】如图,平面直角坐标系xOy中,点A的坐标为(9,6),AB⊥y轴,垂足为B,点P从原点O出发向x轴正方向运动,同时,点Q从点A出发向点B运动,当点Q到达点B时,点P、Q同时停止运动,若点P与点Q的速度之比为1:2,则下列说法正确的是( )
A. 线段PQ始终经过点(2,3)
B. 线段PQ始终经过点(3,2)
C. 线段PQ始终经过点(2,2)
D. 线段PQ不可能始终经过某一定点
查看答案和解析>>
科目:初中数学 来源: 题型:
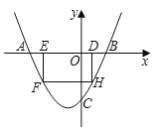
【题目】如图,抛物线![]() 与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
与 x 轴交于点 A、B,与 y 轴交于点 C,且 OC=2OB, 点 D 为线段 OB 上一动点(不与点 B 重合),过点 D 作矩形 DEFH,点 H、F 在抛物线上,点 E 在 x 轴 上.
(1)求抛物线的解析式;
(2)当矩形 DEFH 的周长最大时,求矩形 DEFH 的面积;
(3)在(2)的条件下,矩形 DEFH 不动,将抛物线沿着 x 轴向左平移 m 个单位,抛物线与矩形 DEFH的边交于点 M、N,连接 M、N.若 MN 恰好平分矩形 DEFH 的面积,求 m 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过O、A、B三点,A(4,0)B(1,-3),P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)直线PQ与x轴所夹锐角的度数,并求出抛物线的解析式.
(2)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求: PD+DQ的最大值;②PD.DQ的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;
(3)已知PA=a,PB=b,求PC的长(用含a和b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若cos∠BAE=![]() ,AB=5,求OE的长.
,AB=5,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校共有六个年级,每个年级 10 个班,每个班约 40 名同学.该校食堂共有 10 个窗口中午所有同学都在食堂用餐.经了解,该校同学年龄分布在 12 岁(含 12 岁)到 18岁(含 18 岁)之间,平均年龄 15 岁.小天、小东两位同学,为了解全校同学对食堂各窗口餐食的喜爱情况,各自进行了抽样调查,并记录了相应同学的年龄,每人调查了 60 名同学,将收集到的数据进行了整理.
小天从初一年级每个班随机抽取 6 名同学进行调查,绘制统计图表如下:

小东从全校每个班随机抽取 1 名同学进行调查,绘制统计图表如下:

根据以上材料回答问题:
(1)写出图 2 中 m 的值 ;
(2)小天、小东两人中,哪个同学抽样调查的数据能较好地反映出该校同学对各窗口餐食的喜爱情况,并简要说明另一名同学调查的不足之处;
(3)为使每个同学在中午尽量吃到自己喜爱的餐食,学校餐食管理部门应为 窗口尽 量多的分配工作人员,理由为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com