
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
【答案】(1)9991;221;(2)详见解析;(3)满足条件的所有的四位“言唯一数”为![]() 和
和![]()
【解析】
根据题目给出的新定义,正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,称这样的数k为“言唯一数”,解答即可.
(1)最大的四位“言唯一数”是 9991 ,最小的三位“言唯一数”是 221 ;
(2)证明:设![]() ,则
,则![]()
![]()
![]() 都为正整数,则
都为正整数,则![]() 也是正整数
也是正整数
![]() 对于任意的四位“言唯一数”
对于任意的四位“言唯一数”![]() ,
,![]() 能被
能被![]() 整除.
整除.
(3) ![]()
![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() 、
、![]() 均为整数)
均为整数)
![]() .
.
则![]()
![]()
![]()
![]() 仍然为言唯一数,
仍然为言唯一数, ![]() 末尾数字为0,129末尾数字为9
末尾数字为0,129末尾数字为9
则![]() 的末尾数字为2,
的末尾数字为2,
![]() 或
或![]()
①当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,此时
,此时![]()
②当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,此时
,此时![]()
![]() 满足条件的所有的四位“言唯一数”为
满足条件的所有的四位“言唯一数”为![]() 和
和![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)当t为何值时,△PAE为直角三角形?
(2)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5,它们除数字外没有任何区别.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果.现制定这样一个游戏规则:若所选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
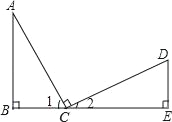
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com