
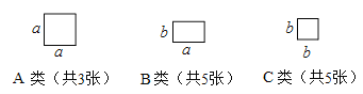
【题目】现有3张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类),5张边长为
类),5张边长为![]() 的矩形纸片(
的矩形纸片(![]() 类),5张边长为
类),5张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类).
类).
我们知道:多项式乘法的结果可以利用图形的面积表示.
例如:![]() 就能用图①或图②的面积表示.
就能用图①或图②的面积表示.
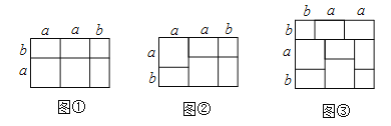
(1)请你写出图③所表示的一个等式:_______________;
(2)如果要拼一个长为![]() ,宽为
,宽为![]() 的长方形,则需要
的长方形,则需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张;
类纸片_____张;
(3)从这13张纸片中取出若干张,每类纸片至少取出一张,把取出的这些纸片拼成一个正方形(按原纸张进行无缝隙,无重叠拼接),则拼成的正方形的边长最长可以是_______(用含![]() 的式子表示).
的式子表示).
【答案】(1)![]() ;(2)1,4,3;(3)
;(2)1,4,3;(3)![]()
【解析】
(1)从整体和部分两方面表示该长方形的面积即可;
(2)根据拼成前后长方形的面积不变可先算出该长方形的面积再确定A类B类C类纸片的张数;
(3)由A类B类C类纸片的张数及面积可知构成的正方形的面积最大为![]() ,利用完全平方公式可得边长.
,利用完全平方公式可得边长.
解:(1)从整体表示该图形面积为![]() ,从部分表示该图形面积为
,从部分表示该图形面积为![]() ,所以可得
,所以可得![]() ;
;
(2)该长方形的面积为![]() ,A类纸片的面积为
,A类纸片的面积为![]() ,B类纸片的面积为
,B类纸片的面积为![]() ,C类纸片的面积为
,C类纸片的面积为![]() ,所以需要
,所以需要![]() 类纸片1张,需要
类纸片1张,需要![]() 类纸片4张,需要
类纸片4张,需要![]() 类纸片3张;
类纸片3张;
(3)A类纸片的面积为![]() ,有3张;B类纸片的面积为
,有3张;B类纸片的面积为![]() ,有5张;C类纸片的面积为
,有5张;C类纸片的面积为![]() ,有5张,所以能构成的正方形的面积最大为
,有5张,所以能构成的正方形的面积最大为![]() ,因为
,因为![]() ,所以拼成的正方形的边长最长可以是
,所以拼成的正方形的边长最长可以是![]() .
.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-![]() )2 016化为(
)2 016化为(![]() )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
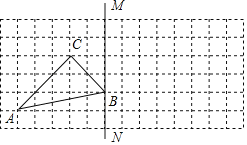
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
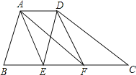
【题目】如图,在梯形![]() 中,
中,![]() 、
、![]() 两点分别在边
两点分别在边![]() 上.
上.![]() ,
,![]() ,且四边形
,且四边形![]() 是平行四边形.
是平行四边形.
![]() 请判断线段
请判断线段![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.
![]() 当
当![]() 时.请猜想四边形
时.请猜想四边形![]() 是什么特殊的平行四边形?并说明理由.
是什么特殊的平行四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AC=BC,∠ACB=90°,以BC为直径作⊙O,连接OA,交⊙O于点D,过D点作⊙O的切线交AC于点E,连接B、D并延长交AC于点F.则下列结论错误的是( )
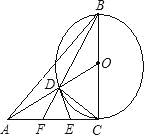
A. △ADE∽△ACO B. △AOC∽△BFC
C. △DEF∽△DOC D. CD2=DFDB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD是边长为1的正方形,O是正方形的中心,Q是边CD上一个动点(点Q不与点C、D重合),直线AQ与BC的延长线交于点E,AE交BD于点P.设DQ=x.
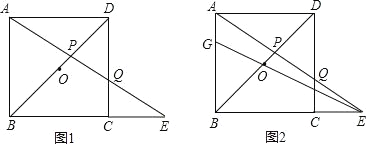
(1)填空:当![]() 时,
时,![]() 的值为 ;
的值为 ;
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:
x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 |
y=x2﹣2x﹣2 | ﹣1.79 | ﹣1.56 | ﹣1.31 | ﹣1.04 | ﹣0.75 | ﹣0.44 | ﹣0.11 | 0.24 | 0.61 |
则一元二次方程x2﹣2x﹣2=0在精确到0.1时一个近似根是 ________ ,利用抛物线的对称性,可推知该方程的另一个近似根是________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆数是( )(参考数据:![]() ,
,![]() ,
,![]() )
)
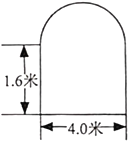
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com