
函数y=3(x﹣2)2+4的图像的顶点坐标是( )
A. (3,4) B. (﹣2,4) C. (2,4) D. (2,﹣4)
C 【解析】函数y=3(x﹣2)2+4的图像的顶点坐标是(2,4).8 故选C.科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:单选题
两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
C 【解析】分两种情况: ①如图所示, ∵木条AB=20cm,CD=24cm, E、F分别是AB、BD的中点, ∴BE=AB=×20=10cm,CF=CD=×24=12cm, ∴EF=EB+CF=10+12=22cm. 故两根木条中点间距离是22cm. ②如图所示, ∵木条AB=20cm,CD=24cm, E、F分别是AB、BD的中点, ...查看答案和解析>>
科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:单选题
下列命题中,不正确的是( )
A. 对角线相等的平行四边形是矩形
B. 有一个角为60°的等腰三角形是等边三角形
C. 直角三角形斜边上的高等于斜边的一半
D. 正方形的两条对角线相等且互相垂直平分
C 【解析】试题分析:根据矩形、等边三角形、直角三角形及正方形的性质进行逐一判断. 【解析】 A、正确,对角线相等的平行四边形是矩形,属于矩形的判定; B、正确,有一个角为60°的等腰三角形是等边三角形属于等边三角形的判定; C、错误,直角三角形斜边上的中线等于斜边的一半; D、正确,是正方形的性质. 故选C.查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:解答题
( 分)如图,点
分)如图,点 、
、 、
、 、
、 在同一直线上,点
在同一直线上,点 、
、 分别在直线
分别在直线 的两侧,且
的两侧,且 ,
,  ,
,  .
.
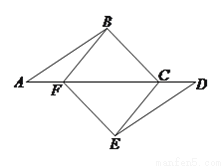
(1)求证:四边形 是平行四边形.
是平行四边形.
( )要使四边形
)要使四边形 为矩形,需要添加一个条件.你可以添加下列条件中的__________.(无需证明)
为矩形,需要添加一个条件.你可以添加下列条件中的__________.(无需证明)
①
②
③连接 ,
, 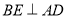
④连接 ,
, 
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:填空题
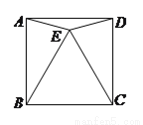
在正方形 内,以
内,以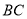 为边作等边
为边作等边 ,连接
,连接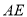 、
、 ,则
,则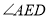 的大小为__________.
的大小为__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
如图所示的几何体的俯视图是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:人教版九年级年级数学下册第二十九章 达标检测卷 题型:填空题
如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC(假定AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确结论的序号是________.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:解答题
先化简,再求值:  (-4x2+2x-8)-(
(-4x2+2x-8)-(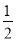 x-1),其中x=
x-1),其中x= .
.
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:单选题
如图,已知AB∥CD,∠2=135°,则∠1的度数是( )

A. 35° B. 45° C. 55° D. 65°
B 【解析】试题分析:∵AB∥CD,∴∠1=∠3,∵∠2=135°,∴∠3=180°﹣135°=45°,∴∠1=45°,故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com