
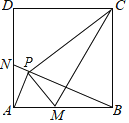
【题目】如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为( )
A.4B.3C.2D.1
【答案】A
【解析】
根据互余角性质得∠PAM=∠PBC,进而得△PAM∽△PBC,可以判断①;
由相似三角形得∠APM=∠BPC,进而得∠CPM=∠APB,从而判断②;
根据对角互补,进而判断③;
由△APB∽△NAB得![]() ,再结合△PAM∽△PBC便可判断④.
,再结合△PAM∽△PBC便可判断④.
解:∵AP⊥BN,
∴∠PAM+∠PBA=90°,
∵∠PBA+∠PBC=90°,
∴∠PAM=∠PBC,
∵∠PMA=∠PCB,
∴△PAM∽△PBC,
故①正确;
∵△PAM∽△PBC,
∴∠APM=∠BPC,
∴∠CPM=∠APB=90°,即PM⊥PC,
故②正确;
∵∠MPC+∠MBC=90°+90°=180°,
∴B、C、P、M四点共圆,
∴∠MPB=∠MCB,
故③正确;
∵AP⊥BN,
∴∠APN=∠APB=90°,
∴∠PAN+∠ANB=90°,
∵∠ANB+∠ABN=90°,
∴∠PAN=∠ABN,
∵∠APN=∠BPA=90°,
∴△PAN∽△PBA,
∴![]() ,
,
∵△PAM∽△PBC,
∴![]() ,
,
∴![]() ,
,
∵AB=BC,
∴AM=AN,
故④正确;
故选:A.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在某建筑物AC上,挂着一宣传条幅BC,站在点F处,测得条幅顶端B的仰角为300,往条幅方向前行20米到达点E处,测得条幅顶端B的仰角为600,求宣传条幅BC的长.(![]() ,结果精确到0.1米)
,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
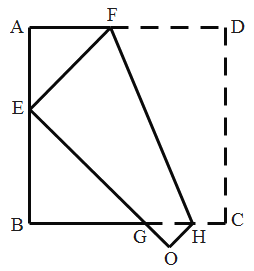
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长是__________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
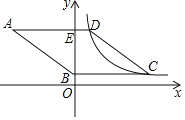
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+4x+5与y轴交于点A,与x轴的正半轴交于点C.
(1)求直线AC解析式;
(2)过点A作AD平行于x轴,交抛物线于点D,点F为抛物线上的一点(点F在AD上方),作EF平行于y轴交AC于点E,当四边形AFDE的面积最大时?求点F的坐标,并求出最大面积;
(3)若动点P先从(2)中的点F出发沿适当的路径运动到抛物线对称轴上点M处,再沿垂直于y轴的方向运动到y轴上的点N处,然后沿适当的路径运动到点C停止,当动点P的运动路径最短时,求点N的坐标,并求最短路径长.
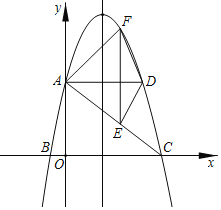
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校决定从甲、乙两名同学中选拔一人参加“诵读经典”大赛,在相同的测试条件下,甲、乙两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83.
乙:88,81,85,81,80.
请回答下列问题:
(1)甲成绩的中位数是______,乙成绩的众数是______;
(2)经计算知![]() ,
,![]() .请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
.请你求出甲的方差,并从平均数和方差的角度推荐参加比赛的合适人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有两条边相等的三角形叫做等腰三角形.类似地,我们定义:至少有一组对边相等的四边形叫做等对边四边形.如图,在△ABC中,AB>AC,点D,E分别在AB,AC上,设CD,BE相交于点O,如果∠A是锐角,∠DCB=∠EBC=![]() ∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
∠A.探究:满足上述条件的图形中是否存在等对边四边形,并证明你的结论.
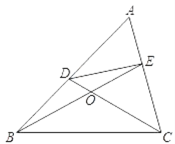
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,BC=BD=10,CD=4,AD=6.点P是线段BD上的动点,点E、Q分别是线段DA、BD上的点,且DE=DQ=BP,联结EP、EQ.
(1)求证:EQ∥DC;
(2)如果△EPQ是以EQ为腰的等腰三角形,求线段BP的长;
(3)当BP=m(0<m<5)时,求∠PEQ的正切值.(用含m的式子表示)
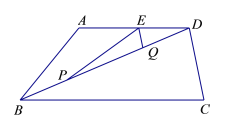
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上有一点C,在AB的同侧作等腰△ACD和等腰△ECB,且AC=AD,EC=EB,∠DAC=∠CEB,直线BD与线段AE,线段CE分别交于点F,G.对于下列结论:①△DCG∽△BEG;②△ACE∽△DCB;③GF·GB=GC·GE;④若∠DAC=∠CEB=90°,则2AD2=DF·DG.其中正确的是( )
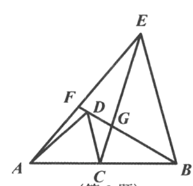
A.①②③④B.①②③C.①③④D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com