
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
如图,E、F是平行四边形对角线AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.判定平行四边形的方法很多,在具体应用时,到底 用哪种方法更好呢?
用哪种方法更好呢?
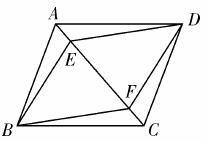
小明、小华、小 颖三位同学对此题进行探讨,给出了各自不同的证明如下:
颖三位同学对此题进行探讨,给出了各自不同的证明如下:
小明的证明方法:
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠DAE=∠BCF.
又 AE=CF,
∴ △AED≌△CFB.
∴ DE=BF,∠AED=∠CFB.
∴ ∠DEF=∠BFE.
∴  ED∥BF.
ED∥BF.
∴ 四边形BEDF是平行四边形.
小华的证明方法:
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AD=BC.
∴ ∠DAE=∠BCF.
又 AE=CF,
∴ △AED≌△CF B.
B.
∴ DE=BF.
同理可证△ABE≌△CDF.
∴ BE=DF.
∴ 四边形BEDF是平行四边形.
小颖的证明方法:
如图,连接BD交AC于点O.
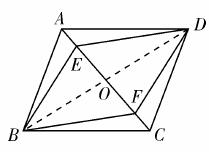
∵ 四边形ABCD是平行四边形,
∴ AO=OC,BO=OD.
又 AE=CF,
∴ OE=OF.
由BO=OD,OE=OF知四边形BEDF是平行四边形.
就这三名同学的证明方法 ,你认为哪一种方法最为简捷?从中你得到什么启示?
,你认为哪一种方法最为简捷?从中你得到什么启示?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是 m(可利用的围墙长度超过6m).

查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线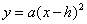 的特点有:
的特点有:
(1)当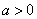 时,开口向 ;当
时,开口向 ;当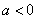 时,开口向 。
时,开口向 。
(2)对称轴是 ,顶点坐标是 。
(3)当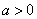 时,在对称轴的左侧(
时,在对称轴的左侧(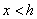 ),
),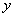 随
随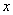 的 ,在对称轴的右侧(
的 ,在对称轴的右侧(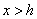 ),
),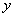 随
随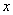 的 ;当
的 ;当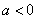 时,在对称轴的左侧(
时,在对称轴的左侧(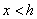 ),
),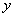 随
随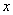 的 ,在对称轴的右侧(
的 ,在对称轴的右侧(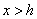 ),
),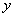 随
随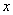 的 。
的 。
(4)当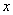 时,函数
时,函数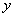 的值最大(或最小),是 。
的值最大(或最小),是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com