
| 1 |
| 2 |
| 5 |
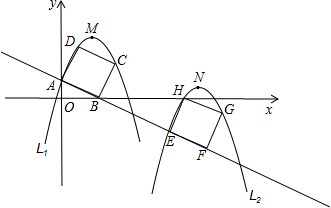
| 1 |
| 2 |
|
| ∥ |
| . |
|
|
| 5 |
| 6 |
| 17 |
| 6 |
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
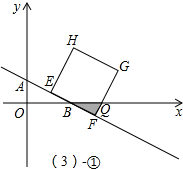
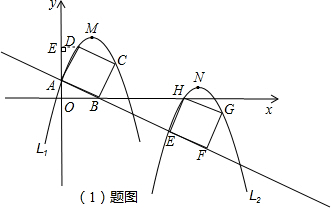
 ∴QF=tan∠QBF•BF=
∴QF=tan∠QBF•BF=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| ||
| 2 |
| 5t2 |
| 4 |
| 5 |
| 5 |
| 5 |
| ||||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 5 |
| 5 |
| 2 |
| 5 |
| 4 |
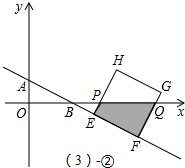
 Rt△HQP中,tan∠HQP=tan∠QBF=
Rt△HQP中,tan∠HQP=tan∠QBF=| 1 |
| 2 |
| 5 |
| ||||
| 2 |
3
| ||||
| 2 |
| HP |
| tan∠HQP |
| 5 |
| 5 |
| 5 |
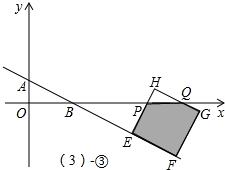
(3
| ||||
| 4 |
| 5 |
| 4 |
| 15 |
| 2 |
| 25 |
| 4 |
| AB |
| BH |
| OA |
| HE |
| ||
| BH |
| 1 | ||
|
| 12 |
| 5 |
| 42 |
| 5 |
17±
| ||
| 10 |
-43-
| ||
| 10 |
-43+
| ||
| 10 |
| 42 |
| 5 |
-43-
| ||
| 10 |
-43+
| ||
| 10 |


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源:不详 题型:解答题
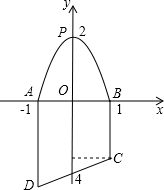
| 线段或抛物线 | 起始坐标 | 关系式 | 终点坐标 |
| 抛物线APB | |||
| 线段BC | (1,0) | x=1 | (1,-1) |
| 线段CD | (1,-1) | ||
| 线段AD | (1,0) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 4 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
 落在点D的位置.
落在点D的位置.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 为租出的车辆数 | 租出的车辆 | ||
| 所有未租出的车每月的维护费 | 租出的车每辆的月收益 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com