练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

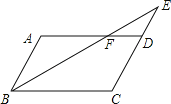
    【题目】如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，CD=2DE．若△DEF的面积为a，则平行四边形ABCD的面积为　 ▲ 　（用a的代数式表示）．

    【答案】12a

    【解析】∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB=CD，

    ∴△DEF∽△CEB，△DEF∽△ABF。

    ∴S△DEF ：S△CE B=（DE：CE）2，S△DEF ：S△ABF=（DE：AB）2，

    ∵CD=2DE，∴DE：CE=1：3，DE：AB=1：2，

    ∵S△DEF=a，∴S△CBE=9a，S△ABF=4a，

    ∴S四边形BCDF=S△CEB﹣S△DEF=8a。∴SABCD=S四边形BCDF+S△ABF=8a+4a=12a

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子，若在铁片的四个角截去四个相同的小正方形，设小正方形的边长为xcm．

    （1）底面的长AB＝　 cm，宽BC＝　 cm（用含x的代数式表示）

    （2）当做成盒子的底面积为300cm2时，求该盒子的容积．

    （3）该盒子的侧面积S是否存在最大的情况？若存在，求出x的值及最大值是多少？若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠ACB＝60○，半径为2的⊙0切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为 （ ）

    A. 2π B. 4π C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．

    （1）求BD的长；

    （2）求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2+2(m+1)x+m21=0.
    (1)若方程有两个不相等的实数根，求实数m的取值范围；
    (2)若方程两实数根分别为x1,x2,且满足x1+x2+x1x2=5，求实数m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，射线BC交⊙O于点D，E是劣弧AD上一点，且，过点E作EF⊥BC于点F，延长FE和BA的延长线交与点G．

    （1）证明：GF是⊙O的切线；

    （2）若AG＝6，GE＝6，求△GOE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球，球面上分别标有数-1，2，-3，4．

    （1）摇匀后任意摸出1个球，则摸出的乒乓球球面上的数是负数的概率为________．

    （2）摇匀后先从中任意摸出1个球（不放回），再从余下的3个球中任意摸出1个球，用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG.

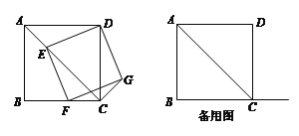
    (1)如图，求证：矩形DEFG是正方形；

    (2)若AB＝2，CE＝2，求CG的长；

    (3)当直线DE与正方形ABCD的某条边所夹锐角是40°时，直接写出∠EFC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某书店销售儿童书刊,一天可出售20套,每套盈利40元.为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多出售2套.设每套降价x元,书店一天可获利润y元.

    (1)求y关于x的函数解析式.

    (2)若要书店每天盈利1200元,则需降价多少元?

    (3)当每套书降价多少元时,书店可获最大利润?最大利润为多少?

    查看答案和解析>>

    同步练习册答案