
分析 根据一元二次方程的解的定义得到:a2+a=$\frac{1}{4}$,a2=$\frac{1}{4}$-a,然后将其代入整理后的所求的代数式进行求值即可.
解答 解:把x=a代入x2+x-$\frac{1}{4}$=0得:a2+a-$\frac{1}{4}$=0,
即a2+a=$\frac{1}{4}$,a2=$\frac{1}{4}$-a,
则$\frac{{a}^{3}-1}{{a}^{5}+{a}^{4}-{a}^{3}-{a}^{2}}$=$\frac{(a-1)({a}^{2}+a+1)}{{a}^{2}(a+1)^{2}(a-1)}$=$\frac{{a}^{2}+a+1}{{a}^{2}({a}^{2}+2a+1)}$=$\frac{\frac{1}{4}+1}{(\frac{1}{4}-a)(\frac{1}{4}+a+1)}$=$\frac{\frac{5}{4}}{\frac{5}{16}-a-{a}^{2}}$=$\frac{\frac{5}{4}}{\frac{5}{16}-\frac{1}{4}}$=20.
点评 本题考查了一元二次方程的解的定义,解题时,利用了“整体代入”的数学思想.


科目:初中数学 来源: 题型:填空题
 如图,⊙O中,直径AB⊥弦CD于点E,弦CG=CD,且交半径OB于点F,射线DG交AB的延长线于点H,若OE=$\frac{4}{3}$,OH=6,则CD=$\frac{4}{3}$$\sqrt{22}$.
如图,⊙O中,直径AB⊥弦CD于点E,弦CG=CD,且交半径OB于点F,射线DG交AB的延长线于点H,若OE=$\frac{4}{3}$,OH=6,则CD=$\frac{4}{3}$$\sqrt{22}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有三条公路L1,L2,L3两两相交,若选择一地点建座加油站,使它到三条公路的距离都相等.应如何选择加油站的地址?这样的地址有几处?
如图所示,有三条公路L1,L2,L3两两相交,若选择一地点建座加油站,使它到三条公路的距离都相等.应如何选择加油站的地址?这样的地址有几处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
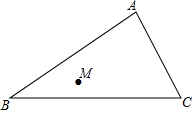 已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称.
已知△ABC及点M,试画出△A1B1C1和△A2B2C2,使△A1B1C1和△ABC关于点M成中心对称,使△A2B2C2和△ABC关于AC所在直线成轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上A、B两点对应的数分别为6和10,点P从原点O出发,以每秒3个单位长度的速度沿数轴正方向运动,同时点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒.
如图,数轴上A、B两点对应的数分别为6和10,点P从原点O出发,以每秒3个单位长度的速度沿数轴正方向运动,同时点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com