练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2005•遵义）如图，把一个边长为6cm的正三角形剪成一个最大的正六边形，则这个正六边形的周长为
    12
    12
    cm．
    分析：根据条件，正三角形剪去正六边形以后剩余三个等边三角形，则正六边形的边长是正三角形的边长的
    1
    3
    ，即可求得边长，则正六边形的周长即可求得．
    解答：解：△ABC和△DEF都是等边三角形，
    则AB=BD=ED=
    1
    3
    AE=2cm，
    则正六边形的周长是：6×2=12cm．
    故答案是：12．
    点评：本题考查了正多边形的计算，注意到正三角形剪去正六边形以后剩余三个等边三角形是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

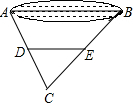    （2005•遵义）如图，A、B两点表示位于一池塘两端的两棵树，为了测量A、B两点间的距离，某同学先在地面上取一个可以直接到达A、B点C，确定AC、BC的中点D、E，并测得DE的长是15米，则A、B的距离为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2005•遵义）如图，⊙O中，弦AB与直径CD相交于点P，且PA=4，PB=6，PD=2，则⊙O的半径为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2005•遵义）如图，在直角坐标系中，经过点A（0，2），B（2，0）和原点O（0，0）三点作⊙C，点P为⊙C上任一点（点P与点O、B不重合），则∠OPB的度数为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

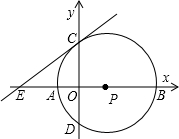    （2005•遵义）如图，点P在x正半轴上，以P为圆心的⊙P与x轴交于A、B两点，与y轴交于C、D两点，⊙P的半径是4，CD=4
    		3
    ．
    （1）过点C作⊙P的切线交x轴于点E，求点E的坐标；
    （2）若
    S△CBO
    S△PCO
    =n    ，求满足下列二个条件的抛物线的解析式：
    ①过点P、E；
    ②抛物线的顶点到x轴的距离为n．

    查看答案和解析>>

    同步练习册答案