
 如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
如图,数轴上的点A,B对应的数分别为-10,5.动点P,Q分别从A,B同时出发,点P以每秒3个单位长度的速度沿数轴向右匀速运动,点Q以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.分析 (1)根据数轴上两点间距离公式可得;
(2)向右运动的点P表示的数在-10的基础上加上其运动路程,向左运动的点Q在5的基础上减去其运动的路程即可;
(3)根据两点间的距离及PQ=$\frac{1}{3}$AB,分P、Q相遇前和P、Q相遇后列方程求解可得.
解答 解:(1)线段AB的长为5-(-10)=15;
(2)点P表示的数为:-10+3t,点Q表示的数为:5-2t;
(3)根据题意,
①点P、点Q相遇前,得:5-2t-(-10+3t)=5,
解得:t=2;
②点P、点Q相遇后,得:-10+3t-(5-2t)=5,
解得:t=4;
综上,t的值为2或4.
点评 本题主要考查两点间的距离及一元一次方程的实际应用能力,根据PQ=$\frac{1}{3}$AB分情况表示出PQ的长是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
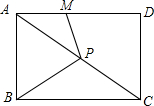 如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.
如图,点P为矩形ABCD的对角线AC上一点,PM⊥PB交AD于M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com