

分析 (1)在Rt△DBC中,根据DB=$\sqrt{D{C}^{2}-B{C}^{2}}$,即可解决问题.
(2)只要证明OM=MF,MF=FT即可.
(3)如图3中,连接OT,在Rt△OTG中利用勾股定理即可解决问题.
(4)分MF为对角线,MF为边两种情形讨论即可.
解答 解:(1)如图1中,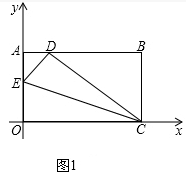
∵|OA-5|+(OC-13)2=0,
又∵|OA-5|≥0,(OC-13)2≥0,
∴OA=5,OC=13,
∵△DEC是由△OEC翻折得到,
∴CD=OC=13,
在Rt△DBC中,DB=$\sqrt{D{C}^{2}-B{C}^{2}}$=12,
∴AD=1,
∴点D坐标(1,5).
(2)如图2中,
∵MF=MO,∠FMN=∠OMN,
∵OM∥ET,
∴∠OMT=∠FTM,
∴∠FMT=∠FTM,
∴FM=FT,
∴OM=FT,∵OA=FG,
∴AM=TG.
(3)如图3中,连接OT,
由(2)可得OT=FT,
由勾股定理可得x2+y2=(5-y)2,
得y=-$\frac{1}{10}$x2+$\frac{5}{2}$.
结合(1)可得AF=OG=1时,x最小,从而x≥1,
当MN恰好平分∠OAB时,AF最大即x最大,
此时G点与N点重合,四边形AONF为正方形,
故x最大为5.
从而x≤5,1≤x≤5.
(4)如图4中,x=3时,y=$\frac{8}{5}$,即点T坐标(3,$\frac{8}{5}$).
∴OM=FT=5-$\frac{8}{5}$=$\frac{17}{5}$,
①当MF为对角线时,点Q与T重合,PM=FT=$\frac{17}{5}$,
∴OP=$\frac{34}{5}$,
∴此时点P坐标(0,$\frac{34}{5}$).
②FM为边时,∵四边形MFQP是平行四边形,
又∵四边形FMOT是平行四边形,
∴点Q与T重合,点P与点O重合,
∴点P坐标(0,0),
综上所述,以M、F、Q、P为顶点的四边形是平行四边形时,点Q坐标(0,0)或(0,$\frac{34}{5}$).
点评 本题考查四边形综合题、矩形的性质、翻折变换、勾股定理、平行四边形的判定等知识,解题的关键是灵活应用这些知识解决问题,学会用分类讨论的思想解决问题,属于中考压轴题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,对角线AC,BD交于点O,EF,HG,MN都过点O,若阴影部分的面积和空白部分的面积分别记为S1和S2,则S1与S2的大小关系为( )
如图,在平行四边形ABCD中,对角线AC,BD交于点O,EF,HG,MN都过点O,若阴影部分的面积和空白部分的面积分别记为S1和S2,则S1与S2的大小关系为( )| A. | S1=S2 | B. | S1>S2 | C. | S1<S2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一个正方形纸片AOCD,放置在平面直角坐标系中,点A(0,4),点O(0,0),点D在第一象限.点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点O落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接OP,OH.设P点的横坐标为m.
如图,将一个正方形纸片AOCD,放置在平面直角坐标系中,点A(0,4),点O(0,0),点D在第一象限.点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点O落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接OP,OH.设P点的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{8+x}{20}$+$\frac{3+x}{30}$=1 | B. | $\frac{x}{20}$+$\frac{x}{30}$=1 | C. | $\frac{8}{20}$+$\frac{3+x}{30}$=1 | D. | $\frac{8+x}{x}$+$\frac{3+x}{30}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com