
【题目】数学活动:探究与发现
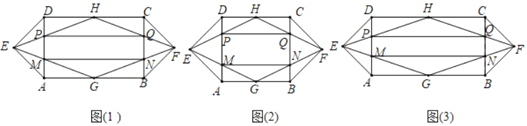
定义:如图(1),四边形ABCD为矩形,△ADE和△BCF均为等腰直角三角形,∠AED=∠BFC=90°,点G、H分别为AB、CD的中点,连接EG、EH、FG、FH,分别与AD、BC交于点M、P、N、Q,我们把四边形PQNM叫做矩形ABCD的递推四边形.
独立思考:
(1)求证:四边形PQNM矩形.
合作交流:
(2)解决完上述问题后,“兴趣”小组的同学们对正方形ABCD的递推四边形进行了探究,如图(2),他们猜想矩形PQNM的宽与长的比![]() .他们猜想的结论是否正确?请说明理由.
.他们猜想的结论是否正确?请说明理由.
发现问题:(3)在“兴趣”小组同学们的启发下,“实践”小组的同学们对宽与长的比为![]() 的矩形的递推四边形进行了探究,如图(3).他们提出如下问题:
的矩形的递推四边形进行了探究,如图(3).他们提出如下问题:
①在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为_____;
,则矩形PQNM的宽与长的比为_____;
②在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为______;
,则矩形PQNM的宽与长的比为______;
③在矩形ABCD中,若![]() ,则矩形PQNM的宽与长的比为______.
,则矩形PQNM的宽与长的比为______.
任务:请你完成“实践”小组提出的数学问题.(注:直接写出结果,不要求说理或证明)
【答案】(1)证明见解析;(2)猜想正确,证明见解析;(3)①1:6;②1:12;③1:n(n+1).
【解析】
(1)根据矩形的判定方法进行证明即可;
(2)如图2中,作EJ⊥AD于J.设正方形的边长为2a.则DH=HC=a,继而求出PM、PQ即可解决问题;
(3)①如图3中,作EJ⊥AD于J.设AD=m,DC=2m,根据等腰直角三角形的性质,平分线分线段成比例的性质,求出PM、PQ即可得;
②作EJ⊥AD于J.设AD=m,DC=3m,求出PM、OQ即可解决问题;
③根据①②探究规律,利用规律解决问题即可.
(1)如图1中,
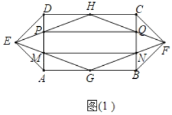
∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,AD=BC,AD∥BC,
∵∠AED=∠BFC=90°,ED=EA,FC=FB,
∴∠ADE=∠EAD=∠FCB=∠FBC=45°,
∴△ADE≌△BFC(ASA),∠EDH=∠FCH=135°
∴DE=FC,
∵DH=CH,
∴△EDH≌△FCH(SAS),
∴∠DHE=∠FHC,
∵∠PDH=∠QCH=90°,
∴△HDP≌△HCQ(ASA),
∴DP=CQ,∵DP∥CQ,
∴四边形DPQC是平行四边形,
∵∠PDC=90°,
∴四边形DPQC是矩形,
∴∠DPQ=∠CQP=90°,
∴∠MPQ=∠NQP=90°,
同法可证:∠PMN=∠QNM=90°,
∴四边形PMNQ是矩形.
(2)结论:猜想正确.
理由:如图2中,作EJ⊥AD于J.设正方形的边长为2a.则DH=HC=a.
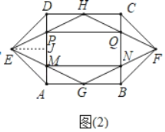
∵ED=EA,∠AED=90°,EJ⊥AD,
∴AJ=DJ=a,
∴EJ=AJ=DJ=a,
∵∠EJP=∠HDP=90°,∠DPH=∠EPJ,DH=EJ=a,
∴△DPH≌△JPE(AAS),
∴DP=PJ,
易证DP=AM,
∴DP=PJ=JM=AM,
∴PM=a,
∵PQ=CD=2a,
∴![]() =
=![]() .
.
(3)①如图3中,作EJ⊥AD于J.设AD=m,DC=2m.
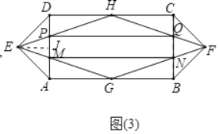
易知:EJ=DJ=AJ=![]() m,DH=CH=m,
m,DH=CH=m,
∵DH∥EJ,
∴![]() =
=![]() =2,
=2,
可得PJ=JM=![]() m,PM=
m,PM=![]() m,PQ=CD=2m,
m,PQ=CD=2m,
∴![]() =
=![]() =
=![]() .
.
②作EJ⊥AD于J.设AD=m,DC=3m.
易知:EJ=DJ=AJ=![]() m,DH=CH=1.5m,
m,DH=CH=1.5m,
∵DH∥EJ,
∴![]() =
=![]() =3,
=3,
可得PJ=JM=![]() m,PM=
m,PM=![]() m,PQ=CD=3m,
m,PQ=CD=3m,
∴![]() =
=![]() =
=![]() .
.
③由①②可知:PM:PQ=1:n(n+1),
故答案为1:6,1:12,1:n(n+1).


科目:初中数学 来源: 题型:
【题目】如图,从一块圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A、B、C在圆周上,将剪下的扇形作为一个圆锥侧面,如果圆锥的高为![]() ,则这块圆形纸片的直径为( )
,则这块圆形纸片的直径为( )
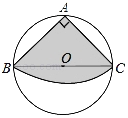
A. 12cm B. 20cm C. 24cm D. 28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(![]() )求本次被调查的学生人数.
)求本次被调查的学生人数.
(![]() )将条形统计图补充完整.
)将条形统计图补充完整.
(![]() )若该校共有
)若该校共有![]() 名学生,请估计全校选择体育类的学生人数.
名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B顺时针旋转90°.得到线段BA1,称点A1为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(﹣2,0)时,点A关于点B的“伴随点”的坐标分别为 , ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
(2)如图2,点C的坐标为(﹣3,0),以C为圆心,![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com