
【题目】小明早晨从家里出发匀速步行去上学.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后t分钟时,他所在的位置与家的距离为s千米,且s与t之间的函数关系的图象如图中的折线段OA﹣AB所示.
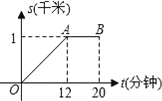
(1)试求折线段OA﹣AB所对应的函数关系式;
(2)请解释图中线段AB的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离s(千米)与小明出发后的时间t(分钟)之间函数关系的图象.(友情提醒:请对画出的图象用数据作适当的标注)
【答案】(1)折线段OA﹣AB所对应的函数关系式为 ;
;
(2)线段AB的实际意义是:小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟;
(3)画出图象见解析.
【解析】分析:(1)OA为正比例函数图象,可以用待定系数法求出;(2)AB段离家距离没发生变化说明在以家为圆心做曲线运动;(3)妈妈的速度正好是小明的2倍,所以妈妈走弧线路用(20-12)÷2=4分钟.
本题解析:(1)线段OA对应的函数关系式为:s=![]() t(0≤t≤12)
t(0≤t≤12)
线段AB对应的函数关系式为:s=1(12<t≤20);
(2)图中线段AB的实际意义是: 小明出发12分钟后,沿着以他家为圆心,1千米为半径的圆弧形道路上匀速步行了8分钟;
(3)由图象可知,小明花20分钟到达学校,则小明的妈妈花20﹣10=10分钟到达学校,可知小明妈妈的速度是小明的2倍,即:小明花12分钟走1千米,则妈妈花6分钟走1千米,故D(16,1),小明花20﹣12=8分钟走圆弧形道路,则妈妈花4分钟走圆弧形道路,故B(20,1). 妈妈的图象经过(10,0)(16,1)(20,1)如图中折线段CD﹣DB就是所作图象.

点睛:本题考查了一次函数的应用,通过考查一次函数的应用来考查从图象上获取信息的能力,特别的作一次函数的图象,关键在于确定点,点确定了,连接就可以得到函数图象.


科目:初中数学 来源: 题型:
【题目】在“村村通柏油路”建设中,甲工程队每天筑路200米,乙工程队每天筑路150米,两队共参加了10天建设,铺设路面不少于1850米,则甲队至少参加了_______天建设
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“囧”(jiong)是网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为![]() 的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别是
的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别是![]() 、
、![]() ,剪去的两个小直角三角形的两直角边长也分别为
,剪去的两个小直角三角形的两直角边长也分别为![]() ,
, ![]() .
.
(![]() )用含有
)用含有![]() 、
、![]() 的代数式表示图中“囧”(阴影部分)的面积.
的代数式表示图中“囧”(阴影部分)的面积.
(![]() )当
)当![]() ,
, ![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③有两个角和其中一个角的对边对应相等的两个三角形全等;④有两边和一个角对应相等的两个三角形全等。其中正确的个数有( )
A 1个 B2个 C3个 D4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF 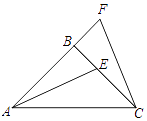
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC =9cm,CB = 6 cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB =![]() cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
cm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足AC![]() BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
BC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com