
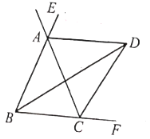
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤
;⑤![]() .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
【答案】①②③⑤
【解析】
根据角平分线定义得出∠ABC=2∠ABD=2∠DBC,∠EAC=2∠EAD,∠ACF=2∠DCF,根据三角形的内角和定理得出∠BAC+∠ABC+∠ACB=180°,根据三角形外角性质得出∠ACF=∠ABC+∠BAC,∠EAC=∠ABC+∠ACB,根据已知结论逐步推理,即可判断各项.
解:∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,∴①正确;
∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,∴②正确;
∵AD平分∠EAC,CD平分∠ACF,
∴∠DAC=![]() ∠EAC,∠DCA=
∠EAC,∠DCA=![]() ∠ACF,
∠ACF,
∵∠EAC=∠ACB+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC=180°,
∴∠ADC=180°-(∠DAC+∠ACD)
=180°-![]() (∠EAC+∠ACF)
(∠EAC+∠ACF)
=180°-![]() (∠ABC+∠ACB+∠ABC+∠BAC)
(∠ABC+∠ACB+∠ABC+∠BAC)
=180°-![]() (180°+∠ABC)
(180°+∠ABC)
=90°-![]() ∠ABC,∴③正确;
∠ABC,∴③正确;
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵∠ADB=∠DBC,∠ADC=90°-![]() ∠ABC,
∠ABC,
∴∠ADB不等于∠CDB,∴④错误;
∵BD平分∠ABC,
∴∠CBD=∠CBD=![]() ∠ABC,
∠ABC,
∵CD平分∠ACF,
∴∠DCF=![]() ∠ACF,
∠ACF,
∴∠DCF-∠CBD=![]() ∠ACF-
∠ACF-![]() ∠ABC
∠ABC
∵∠BAC=∠ACF-∠ABC
∠BDC=∠DCF-∠CBD
∴∠BDC=![]() ∠BAC,⑤正确.
∠BAC,⑤正确.
故答案为:①②③⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,求大楼AB的高度是多少?(精确到0.1米,参考数据:
,求大楼AB的高度是多少?(精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )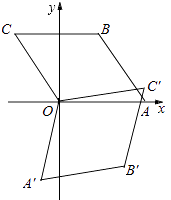
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.


(1)若∠H=120°,则∠H的4系补周角的度数为 ;
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.

(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
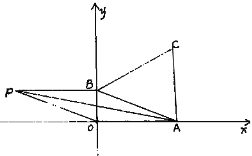
【题目】如图一次函数![]() 的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形ABC,
的图象与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等边三角形ABC,
(1)求![]() ABC的面积。
ABC的面积。
(2)如果在第二象限内有一点P(![]() ),试用含有a的代数式表示四边形ABPO的面积,并求出当
),试用含有a的代数式表示四边形ABPO的面积,并求出当![]() ABP的面积与
ABP的面积与![]() ABC的面积相等时a的值。
ABC的面积相等时a的值。
(3)在x轴上,是否存在点M,使![]() MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com