
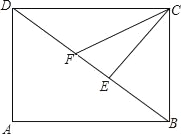
【题目】如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF的长.
【答案】(1)见解析,(2)CF=![]() cm.
cm.
【解析】
(1)要求证:BF=BC只要证明∠CFB=∠FCB就可以,从而转化为证明∠BCE=∠BDC就可以;
(2)已知AB=4cm,AD=3cm,就是已知BC=BF=3cm,CD=4cm,在直角△BCD中,根据三角形的面积等于![]() BDCE=
BDCE=![]() BCDC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理就可以求出,由此解决问题.
BCDC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理就可以求出,由此解决问题.
证明:(1)∵四边形ABCD是矩形,∴∠BCD=90°,
∴∠CDB+∠DBC=90°.
∵CE⊥BD,∴∠DBC+∠ECB=90°.
∴∠ECB=∠CDB.
∵∠CFB=∠CDB+∠DCF,∠BCF=∠ECB+∠ECF,∠DCF=∠ECF,
∴∠CFB=∠BCF
∴BF=BC
(2)∵四边形ABCD是矩形,∴DC=AB=4(cm),BC=AD=3(cm).
在Rt△BCD中,由勾股定理得BD=![]() .
.
又∵BDCE=BCDC,
∴CE=![]() .
.
∴BE=![]() .
.
∴EF=BF﹣BE=3﹣![]() .
.
∴CF=![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.
(1)A,B两种型号的自行车的单价分别是多少?
(2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 过点(-2,5),和直线
过点(-2,5),和直线![]() ,分别在下列条件下求这个一次函数的解析式.
,分别在下列条件下求这个一次函数的解析式.
(1)它的图象与直线![]() 平行;
平行;
(2)它的图象与y轴的交点和直线![]() 与y轴的交点关于
与y轴的交点关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道,![]() ,类似地,我们把
,类似地,我们把![]() 看成一个整体,则
看成一个整体,则![]()
![]() .“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
.“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把![]() 看成一个整体,合并
看成一个整体,合并![]() 的结果是______________.
的结果是______________.
(2)当![]() 时,代数式
时,代数式![]() 的值为
的值为![]() ,则当
,则当![]() 时,求代数式
时,求代数式![]() 的值.
的值.
拓广探索:
(3)已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
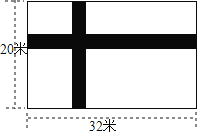
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从原点出发以每秒
从原点出发以每秒![]() 个单位长度的速度沿负方向运动,动点
个单位长度的速度沿负方向运动,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为
个单位的速度先沿正方向运动,到达原点后立即按原速反方向运动,三点同时出发,出发时间为![]() (秒).
(秒).

(1)点![]() 在数轴上所表示的数分别为:____________,____________;
在数轴上所表示的数分别为:____________,____________;
(2)当![]() 两点重合时,求此时点
两点重合时,求此时点![]() 在数轴上所表示的数;
在数轴上所表示的数;
查看答案和解析>>
科目:初中数学 来源: 题型:
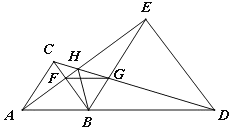
【题目】如图所示,已知△ABC和△BDE都是等边三角形。下列结论:① AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°,⑤△BFG是等边三角形;⑥ FG∥AD。其中正确的有_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
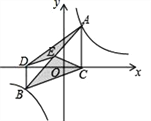
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
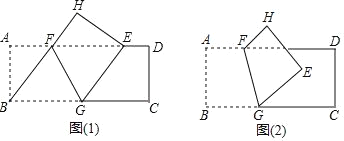
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,顶点B的对应点为E.
(1)如图(1),当顶点B的对应点E落在边AD上时.
①连接BF,试判断四边形BGEF是怎样的特殊四边形,并说明理由;
②若BG=10,求折痕FG的长;
(2)如图(2),当顶点B的对应点E落在长方形内部,E到AD的距离为2,且BG=10时,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com