
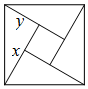
 如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )
如图,是4个全等的直角三角形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两条直角边(x>y),请观察图案,指出下列关系式不正确的是( )| A. | x2+y2=49 | B. | x-y=2 | C. | 2xy+4=49 | D. | x+y=13 |
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
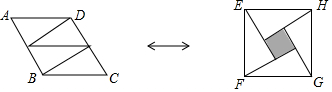
| A. | 1 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
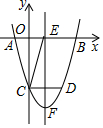 如图,抛物线y=x2+mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C.抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是D,以点B,C,D,E为顶点作四边形,设以点B,C,D,E为顶点的四边形的面积为S.
如图,抛物线y=x2+mx+n经过点A(-1,0),与x轴的另一个交点是B(B在A的右侧),与y轴交于点C.抛物线的对称轴EF交x轴于点E,点C关于EF的对称点是D,以点B,C,D,E为顶点作四边形,设以点B,C,D,E为顶点的四边形的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:
甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
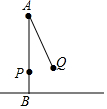 如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)
如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com