
分析 连接两个已知点的线段有3条,作它们的垂直平分线,在这些垂直平分线及已知3个点外,任取一点O为圆心.设O到这3个已知的距离为d1,d2,d3,则它们两两不等且都大于0.接下来只要证明可以取得r0,r1,r2,r3为半径的同心圆满足所有的要求即可.
解答 证明:连接两个已知点的线段有3条,作它们的垂直平分线,在这些垂直平分线及已知3个点外,任取一点O为圆心.
设O到这3个已知的距离为d1,d2,d3,则它们两两不等且都大于0.
不妨假设0<d1<d2<d3,则存在有理数r1,r2,r3,使得d1<r1<d2<r2<d3<r3,
将它们通分得r1=$\frac{{P}_{1}}{M}$,r2=$\frac{{P}_{2}}{M}$,r3=$\frac{{P}_{3}}{M}$,这里M是它们分母的公倍数.
我们可以取M足够大,使$\frac{1}{M}$<d1,
令r0=$\frac{1}{M}$,则以r0,r1,r2,r3为半径的同心圆满足所有的要求.
点评 本题考查圆综合题、线段的垂直平分线的性质、同心圆等知识,解题的关键是理解题意,本题的突破点是取点O在这些垂直平分线及已知3个点外,这是关键,题目比较抽象,属于属于竞赛题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{90}{x+2}$=$\frac{60}{x-2}$ | B. | $\frac{90}{x-2}$=$\frac{60}{x+2}$ | C. | $\frac{90}{x}$+2=$\frac{60}{x}$ | D. | $\frac{60}{x}$+2=$\frac{90}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
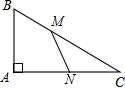 如图,Rt△ABC中,∠A=90°,∠ABC=60°,AC=3,点M是边BC上一点,点N是边AC上一点(不与点A、C重合),且MB=MN,则MB的取值范围是$\frac{2\sqrt{3}}{3}$≤MB<$\sqrt{3}$.
如图,Rt△ABC中,∠A=90°,∠ABC=60°,AC=3,点M是边BC上一点,点N是边AC上一点(不与点A、C重合),且MB=MN,则MB的取值范围是$\frac{2\sqrt{3}}{3}$≤MB<$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
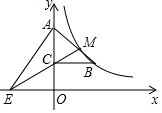 如图,反比例函数y=$\frac{k}{x}$的图象经过Rt△ABC斜边AB的中点M 及顶点B,点C在y轴正半轴上,连结MC并延长与x轴交于点E.
如图,反比例函数y=$\frac{k}{x}$的图象经过Rt△ABC斜边AB的中点M 及顶点B,点C在y轴正半轴上,连结MC并延长与x轴交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com