练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．下列图形中既是轴对称图形，又是中心对称图形的是（　　）
    A．B．C．D．

    分析 根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．

    解答 解：A、不是轴对称图形，是中心对称图形，故本选项错误；
    B、是轴对称图形，不是中心对称图形，故本选项错误；
    C、是轴对称图形，不是中心对称图形，故本选项错误；
    D、既是轴对称图形，又是中心对称图形，故本选项正确．
    故选D．

    点评 本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知x2-4x-3=0，求代数式（2x-3）2-（x+2）（x-2）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：$\sqrt{8}$一4sin45°+（3-π）0+|-4|+${（-\frac{1}{2}）}^{-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

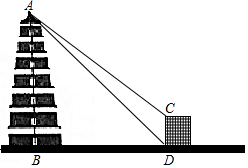    12．“大雁塔”是西安市的标志性建筑、著名古迹、唐代永徽三年，玄樊为藏经典而修建，塔身七层，被视为古都西安的象征．民间人士道：“不到大雁塔，不算到西安”．小明在学习了锐角三角函数后，想用所学知识测量“大雁塔”的高度，小明在一栋高15米的建筑物底部D处侧得塔顶端A的仰角为45°，接着在建筑物顶端C处测得塔顶端A的仰角为37.5°．已知AB⊥BD，CD⊥BD，请你根据题中提供的相关信息，求出“大雁塔”的高AB的长度．（结果精确到0.1米）（参考数据：sin37.5°≈0.6088，cos37.5°≈0.7934，tan37.5°≈0.7673．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

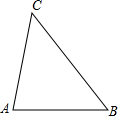    19．如图，在△ABC中，∠A＞∠B．
    （1）作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；
    （2）在（1）的条件下，连接AE，若∠B=50°，求∠AEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．在现实生活中，我们经常会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为$\sqrt{2}$：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P为DC边上一定点，且CP=BC，如图所示．

    （1）如图①，求证：BA=BP；
    （2）如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求$\frac{CG}{GB}$的值；
    （3）如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

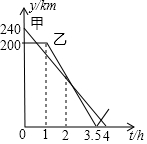    16．在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地．在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h时，两车相遇；②乙车出发1.5h时，两车相距170km；③乙车出发2$\frac{5}{7}$h时，两车相遇；④甲车到达C地时，两车相距40km．其中正确的是②③④（填写所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

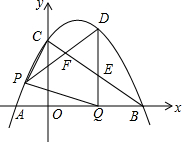    13．如图，抛物线y=-$\frac{\sqrt{3}}{9}$x2+$\frac{2\sqrt{3}}{3}$x+3$\sqrt{3}$与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．
    （1）求直线BC的函数表达式；
    （2）①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）
    ②在点P、Q运动的过程中，当PQ=PD时，求t的值；
    （3）试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某中学艺术节期间，学校向学生征集书画作品，杨老师从全校30个班中随机抽取了4个班（用A，B，C，D表示），对征集到的作品的数量进行了分析统计，制作了两幅不完整的统计图．

    请根据以上信息，回答下列问题：
    （1）杨老师采用的调查方式是抽样调查（填“普查”或“抽样调查”）；
    （2）请你将条形统计图补充完整，并估计全校共征集多少件作品？
    （3）如果全校征集的作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生，现要在获得一等奖的作者中选取两人参加表彰座谈会，请你用列表或树状图的方法，求恰好选取的两名学生性别相同的概率．

    查看答案和解析>>

    同步练习册答案