
ΓΨΧβΡΩΓΩ‘ΎΧΫΨΩ»ώΫ«»ΐΫ«Κ· ΐΒΡ“β“εΒΡ―ßœΑΙΐ≥Χ÷–Θ§–ΓΝΝΖΔœ÷ΘΚΓΑ»γΆΦ1Θ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§Ω…ΧΫΨΩΒΟΒΫ
Θ§Ω…ΧΫΨΩΒΟΒΫ![]() Γ±
Γ±
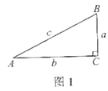
Θ®1Θ©«κΡψάϊ”ΟΆΦ1ΧΫΨΩΥΒΟς–ΓΝΝΒΡΥΒΖ® «Ζώ’ΐ»ΖΘΜ
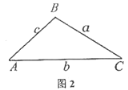
Θ®2Θ©–Γάω≤¬œκΓΑ»γΙϊ‘ΎΕέΫ«»ΐΫ«–Έ÷–Θ§ΝΫΗω»ώΫ«’ΐœ“÷Β”κΥϋΟ«ΥυΕ‘±ΏΒΡ±Ώ≥Λ÷°Φδ“≤”–“ΜΕ®ΒΡΙΊœΒΓΑ‘ΎΆΦ2ΒΡΕέΫ«![]() ÷–Θ§
÷–Θ§![]() «ΕέΫ«Θ§«κΡψάϊ”ΟΆΦ2Αο–ΓάωΧΫΨΩ
«ΕέΫ«Θ§«κΡψάϊ”ΟΆΦ2Αο–ΓάωΧΫΨΩ![]() ”κ
”κ![]() ÷°ΦδΒΡΙΊœΒΘ§≤Δ–¥≥ωΧΫΨΩΙΐ≥ΧΘ°
÷°ΦδΒΡΙΊœΒΘ§≤Δ–¥≥ωΧΫΨΩΙΐ≥ΧΘ°
Θ®3Θ©‘Ύ»ώΫ«![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷°Φδ¥φ‘Ύ ≤Ο¥ΙΊœΒΘ§«κΡψΧΫΨΩ≤Δ÷±Ϋ”–¥≥ωΫα¬έΘ°
÷°Φδ¥φ‘Ύ ≤Ο¥ΙΊœΒΘ§«κΡψΧΫΨΩ≤Δ÷±Ϋ”–¥≥ωΫα¬έΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©–ΓΝΝΥΒΖ®’ΐ»ΖΘΜΘ®2Θ©![]() Θ§ΧΫΨΩΙΐ≥ΧΦϊΫβΈωΘΜΘ®3Θ©
Θ§ΧΫΨΩΙΐ≥ΧΦϊΫβΈωΘΜΘ®3Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷±πάϊ”ΟΓœAΘ§ΓœBΒΡ’ΐœ“÷Β«σ≥ω–±±ΏcΒΡ≥ΛΕ»Θ§¥”Εχ≈–Εœ–ΓΝΝΒΡΥΒΖ® «Ζώ’ΐ»ΖΘΜ
Θ®2Θ©ΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() ΒψΘ§άϊ”ΟΓœAΘ§ΓœCΒΡ’ΐœ“÷Β«σ≥ωBDΒΡ≥ΛΘ§¥”ΕχΒΟΒΫ
ΒψΘ§άϊ”ΟΓœAΘ§ΓœCΒΡ’ΐœ“÷Β«σ≥ωBDΒΡ≥ΛΘ§¥”ΕχΒΟΒΫ![]() Θ§ΫΪΒ» ΫΫχ––±δ–ΈΒΟΒΫΫα¬έΘΜ
Θ§ΫΪΒ» ΫΫχ––±δ–ΈΒΟΒΫΫα¬έΘΜ
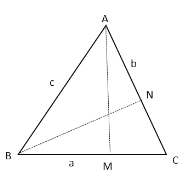
Θ®3Θ©ΙΐΒψAΉςAMΓΆBCΘ§ΙΐΒψBΉςBNΓΆACΘ§Ζ÷±π‘ΎRtΓςABMΚΆRtΓςACM÷–«σ≥ω![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() Θ§‘ΎRtΓςABNΚΆRtΓςBCM÷–Θ§«σ≥ω
Θ§‘ΎRtΓςABNΚΆRtΓςBCM÷–Θ§«σ≥ω![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() Θ§¥”ΕχΈ ΧβΒΟΫβΘ°
Θ§¥”ΕχΈ ΧβΒΟΫβΘ°
ΫβΘΚΘ®1Θ©ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§![]()
Γύ![]()
ΓΏ![]()
Γύ![]()
Γύ![]()
Γύ–ΓΝΝΥΒΖ®’ΐ»ΖΘΜ
Θ®2Θ©ΫβΘΚΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() ΒψΘ§
ΒψΘ§
ΓΏ![]() ‘Ύ
‘Ύ![]() ÷–Θ§
÷–Θ§![]()
Γύ![]()
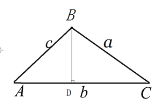
ΓΏ‘Ύ![]() ÷–Θ§
÷–Θ§![]()
Γύ![]()
Γύ![]()
Γύ![]() ΘΜ
ΘΜ
Θ®3Θ©ΙΐΒψAΉςAMΓΆBCΘ§ΙΐΒψBΉςBNΓΆAC
‘ΎRtΓςABMΚΆRtΓςACM÷–Θ§![]()
Γύ![]()
‘ΎRtΓςABNΚΆRtΓςBCM÷–Θ§![]()
Γύ![]()
Γύ![]()
Φ¥![]() Θ°
Θ°


 ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΟΩ»’10Ζ÷÷”ΩΎΥψ–ΡΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2018Ρξ10‘¬23»’Θ§Ηέ÷ιΑΡ¥σ«≈’ΐ ΫΩΣΆ®Θ§≥…ΈΣΚαΊ®‘ΎΝφΊξ―σ…œΒΡ“ΜΒάωΠάωΒΡΖγΨΑ.¥σ«≈÷ςΧεΙΛ≥ΧΥμΒάΒΡΕΪΓΔΈςΝΫΕΥΗς…η÷ΟΝΥ“ΜΗωΚΘ÷–»ΥΙΛΒΚΘ§ά¥œΈΫ”«≈ΝΚΚΆΚΘΒΉΥμΒάΘ§Ές»ΥΙΛΒΚ…œΒΡAΒψΚΆΕΪ»ΥΙΛΒΚ…œΒΡBΒψΦδΒΡΨύάκ‘ΦΈΣ5.6«ßΟΉΘ§ΒψC «”κΈς»ΥΙΛΒΚœύΝ§ΒΡ¥σ«≈…œΒΡ“ΜΒψΘ§AΘ§BΘ§C‘Ύ“ΜΧθ÷±œΏ…œΘ°»γΆΦΘ§“ΜΥ“ΙέΙ⥧―Ί”κ¥σ«≈![]() ΕΈ¥Ι÷±ΒΡΖΫœρΚΫ––Θ§ΒΫ¥οPΒψ ±Ιέ≤βΝΫΗω»ΥΙΛΒΚΘ§Ζ÷±π≤βΒΟ
ΕΈ¥Ι÷±ΒΡΖΫœρΚΫ––Θ§ΒΫ¥οPΒψ ±Ιέ≤βΝΫΗω»ΥΙΛΒΚΘ§Ζ÷±π≤βΒΟ![]() ”κΙέΙ⥧ΚΫœρ
”κΙέΙ⥧ΚΫœρ![]() ΒΡΦ–Ϋ«ΓœDPA=18ΓψΘ§ΓœDPB=53ΓψΘ§«σ¥Υ ±ΙέΙ⥧ΒΫ¥σ«≈ACΕΈΒΡΨύάκ
ΒΡΦ–Ϋ«ΓœDPA=18ΓψΘ§ΓœDPB=53ΓψΘ§«σ¥Υ ±ΙέΙ⥧ΒΫ¥σ«≈ACΕΈΒΡΨύάκ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ΈΩΦ ΐΨίΘΚ![]() Γψ
Γψ![]() Θ§
Θ§![]() Γψ
Γψ![]() Θ§
Θ§![]() Γψ
Γψ![]() Θ§
Θ§![]() Γψ
Γψ![]() Θ§
Θ§![]() Γψ
Γψ![]() Θ§
Θ§![]() Γψ
Γψ![]() Θ°
Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–ΒΡΒψPΚΆΓ―MΘ§Ηχ≥ω»γœ¬Ε®“εΘΚ»τΓ―M…œ¥φ‘ΎΝΫΗωΒψAΘ§BΘ§ ΙAB=2PMΘ§‘ρ≥ΤΒψPΈΣΓ―MΒΡΓΑΟάΚΟΒψΓ±Θ°
Θ®1Θ©Β±Γ―MΑκΨΕΈΣ2Θ§ΒψMΚΆΒψO÷ΊΚœ ±Θ°
ΔΌΒψP1(©¹2Θ§0)Θ§P2(1Θ§1)Θ§P3(2Θ§2)÷–Θ§Γ―OΒΡΓΑΟάΚΟΒψΓ± «ΓΓΓΓΓΓΓΓΘΜ
ΔΎ»τ÷±œΏy=2x+b…œ¥φ‘ΎΒψPΈΣΓ―OΒΡΓΑΟάΚΟΒψΓ±Θ§«σbΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©ΒψMΈΣ÷±œΏy=4…œ“ΜΕ·ΒψΘ§“‘2ΈΣΑκΨΕΉςΓ―MΘ§ΒψPΈΣ÷±œΏy=x…œ“ΜΕ·ΒψΘ§ΒψPΈΣΓ―MΒΡΓΑΟάΚΟΒψΓ±Θ§«σΒψMΒΡΚαΉχ±ξmΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§ΒψGΈΣΕ‘Ϋ«œΏAC…œ“ΜΒψΘ§AG=ABΘ°ΓœCAE=15Γψ«“AE=ACΘ§Ν§Ϋ”GEΘ°ΫΪœΏΕΈAE»ΤΒψAΡφ ±’κ–ΐΉΣΒΟΒΫœΏΕΈAFΘ§ ΙDF=GEΘ§‘ρΓœCAFΒΡΕ» ΐΈΣ________Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() ΒΡΉχ±ξ «
ΒΡΉχ±ξ «![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξ «
ΒΡΉχ±ξ «![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§ΫΪ
ΒΡ÷–ΒψΘ§ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Ρφ ±’κ–ΐΉΣ
Ρφ ±’κ–ΐΉΣ![]() ΚσΒΟΒΫ
ΚσΒΟΒΫ![]() Θ§»τΖ¥±»άΐΚ· ΐ
Θ§»τΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσ«ΓΚΟΨ≠Ιΐ
ΒΡΆΦœσ«ΓΚΟΨ≠Ιΐ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷Β «Θ® Θ©
ΒΡ÷Β «Θ® Θ©

A.24B.25C.26D.30
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥφΉ≈Ψ≠ΦΟΒΡΩλΥΌΖΔ’ΙΘ§ΜΖΨ≥Έ Χβ‘Ϋά¥‘Ϋ ήΒΫ»ΥΟ«ΒΡΙΊΉΔΘ°ΈΣΝΥΝΥΫβά§ΜχΖ÷άύ÷Σ ΕΒΡΤ’ΦΑ«ιΩωΘ§Ρ≥–ΘΥφΜζΒς≤ιΝΥ≤ΩΖ÷―ß…ζΘ§Βς≤ιΫαΙϊΖ÷ΈΣΓΑΖ«≥ΘΝΥΫβΓ±ΓΔΓΑΝΥΫβΓ±ΓΔΓΑΝΥΫβΫœ…ΌΓ±ΓΔΓΑ≤ΜΝΥΫβΓ±ΥΡάύΘ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…œ¬ΟφΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
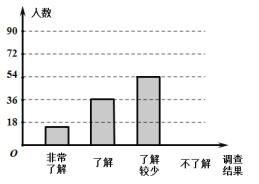
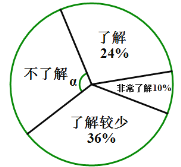
Θ®1Θ©±Ψ¥Έ±ΜΒς≤ιΒΡ―ß…ζ”– ΟϊΘ§…»–ΈΆ≥ΦΤΆΦ÷–Θ§![]()
Θ®2Θ©ΫΪΧθ–ΈΆ≥ΦΤΆΦ Θ”ύΒΡ≤ΩΖ÷≤Ι≥δΆξ’ϊΘ®Αϋά®÷λ±ξΦ«ΒΡ ΐΨίΘ©
Θ®3Θ©ΙάΦΤΗΟ–Θ![]() Οϊ―ß…ζ÷–ΓΑΖ«≥ΘΝΥΫβΓ±”κΓΑΝΥΫβΓ±ΒΡ»Υ ΐΚΆ «Εύ…ΌΘ°
Οϊ―ß…ζ÷–ΓΑΖ«≥ΘΝΥΫβΓ±”κΓΑΝΥΫβΓ±ΒΡ»Υ ΐΚΆ «Εύ…ΌΘ°
Θ®4Θ©Ρ≥ΜΖ±Θ–ΓΕ””–3ΟϊΡ–…ζΘ§1Οϊ≈°…ζΘ§¥”÷–ΥφΜζ≥ι»Γ2»Υ‘Ύ»Ϊ–ΘΉωά§ΜχΖ÷άύ÷Σ ΕΫΜΝςΘ§«σ«ΓΚΟ≥ιΒΫ“ΜΡ–“Μ≈°ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚΓςABC»ΐΗωΕΞΒψΒΡΉχ±ξΖ÷±πΈΣAΘ®©¹2Θ§©¹2Θ©Θ§BΘ®©¹5Θ§©¹4Θ©Θ§CΘ®©¹1Θ§©¹5Θ©Θ°
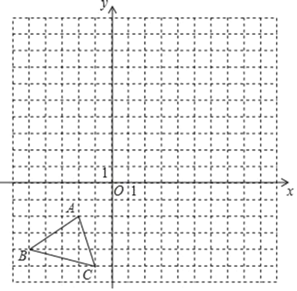
Θ®1Θ©Μ≠≥ωΓςABCΙΊ”Ύx÷αΕ‘≥ΤΒΡΓςA1B1C1ΘΜ
Θ®2Θ©“‘ΒψOΈΣΈΜΥΤ÷––ΡΘ§ΫΪΓςABCΖ≈¥σΈΣ‘≠ά¥ΒΡ2±ΕΘ§ΒΟΒΫΓςA2B2C2Θ§«κ‘ΎΆχΗώ÷–Μ≠≥ωΓςA2B2C2Θ°
Θ®3Θ©ΔΌΒψB1ΒΡΉχ±ξΈΣΓΓ ΓΓΘΜΔΎ«σΓςA2B2C2ΒΡΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§AB=8Θ§AD=6Θ§PΈΣ…δœΏAB…œ“ΜΗωΕ·ΒψΘ§ΙΐPΉςPFΓΆACΘ§¥ΙΉψΈΣFΘ§ΫΜCD”ΎΒψGΘ§Ν§Ϋ”CP”κBFΫΜ”ΎΒψHΘ§ΙΐΒψCΘ§PΘ§FΉςΓ―OΘ°

Θ®1Θ©Β±AP=5 ±Θ§«σ÷ΛΘΚΓœCPB=ΓœFBCΘ°
Θ®2Θ©Β±ΒψP‘ΎœΏΕΈAB…œ ±Θ§»τΓςFCHΒΡΟφΜΐΒ»”ΎΓςPBHΟφΜΐΒΡ4±ΕΘ§«σDGΒΡ≥ΛΘ°
Θ®3Θ©Β±Γ―O”κΓςADCΒΡΤδ÷–“Μ±Ώœύ«– ±Θ§«σΥυ”–¬ζΉψΧθΦΰΒΡAPΒΡ≥ΛΘ°
Θ®4Θ©Β±HΫΪœΏΕΈCPΖ÷≥…1ΘΚ4ΒΡΝΫ≤ΩΖ÷ ±Θ§«σAPΒΡ≥Λ(÷±Ϋ”–¥≥ωΫαΙϊ)Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2020Ρξ≥θΘ§ ή–¬ΙΎΖΈ―Ή“Ώ«ιΒΡ”ΑœλΘ§»ΪΙζΗς÷––Γ―ßΕΦ≤…»ΓΝΥœΏ…œ―ßœΑΖΫ ΫΘ°ΈΣΝΥΫβΨ≈ΡξΦΕ―ß…ζΆχ…œ―ßœΑΒΡ–ßΙϊΘ§ΦΉΓΔ““ΝΫΗω―ß–ΘΆ§ ±≤ΈΦ”ΝΥ“Μ¥ΈœύΆ§ΒΡΆχ…œ≤β ‘Θ§Φ«¬Φ≥…Φ®Θ®ΑΌΖ÷÷ΤΘ©Θ°Ζ÷±π¥”ΦΉΓΔ““ΝΫΥυ―ß–ΘΥφΜζ≥ι»ΓΝΥ20Οϊ―ß…ζΒΡ≤β ‘≥…Φ®Θ§ ΐΨί»γœ¬Θ®ΑΌΖ÷÷ΤΘ©ΘΚ
ΦΉΘΚ63 70 95 84 75 82 78 78 86 96
92 100 52 89 88 84 84 92 90 84
““ΘΚ75 95 85 93 85 92 84 89 96 98
46 86 77 100 100 68 50 85 78 69
’ϊάμ…œΟφΒΡ ΐΨίΘ§ΒΟΒΫ±μΗώ»γœ¬ΘΚ
≤β ‘≥…Φ®Θ®Ζ÷Θ© |
|
|
|
|
|
ΦΉ | 1 | 2 | 3 | 9 | 5 |
““ | 2 | 2 | 3 | 6 | 7 |
―υ±Ψ ΐΨίΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔ÷Ύ ΐ»γœ¬±μΥυ ΨΘΚ
Ά≥ΦΤΝΩ | ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ |
ΦΉ | 83.1 |
| 84 |
““ | 82.4 | 85.5 |
|
ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±μ÷–ΒΡ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©»τΦΉ―ß–ΘΙ≤”–500Οϊ―ß…ζΘ§«κ”Ο―υ±Ψ÷–ΒΡ ΐΨίΙάΦΤΦΉ―ß–ΘΙ≤”–Εύ…Ό»ΥΒΡ≤β ‘≥…Φ®¥οΒΫ”≈–ψΘ®ΙφΕ®ΘΚ≤β ‘≥…Φ®![]() Ζ÷ΈΣ”≈–ψΘ©ΘΜ
Ζ÷ΈΣ”≈–ψΘ©ΘΜ
Θ®3Θ©ΗυΨί“‘…œ ΐΨίΆΤΕœ“ΜΥυΡψ»œΈΣ≥…Φ®ΫœΚΟΒΡ―ß–ΘΘ§≤ΔΥΒΟςάμ”…Θ°Θ®÷Ν…Ό¥”ΝΫΗω≤ΜΆ§ΒΡΫ«Ε»ΫαΚœ ΐΨίΥΒΟςΆΤΕœΒΡΚœάμ–‘Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com