练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．先化简，再求值：（x+2）（x-2）-（x+3）2，其中x=$\frac{1}{3}$．

    分析 原式利用平方差公式，完全平方公式化简，去括号合并得到最简结果，把x的值代入计算即可求出值．

    解答 解：原式=x2-4-x2-6x-9=-6x-13，
    当x=$\frac{1}{3}$时，原式=-2-13=-15．

    点评 此题考查了整式的混合运算-化简求值，熟练掌握平方差公式，以及完全平方公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

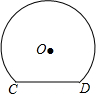    15．如图是一个隧道的横断面，它的形状是以点O为圆心的圆的一部分，如果圆的半径为$\frac{10}{3}$m，弦CD=4m，那么隧道的最高处到CD的距离是（　　）
    A．$\frac{8}{3}$mB．4mC．$\frac{17}{3}$mD．6m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．两块全等的三角板ABC和EDC如图（1）放置，AC=CB，CE=CD，∠ACB=∠ECD=90°，且AB与CE交于F，ED与AB、BC分别交于M、H，△ABC不动，将△EDC绕点C旋转到如图（2），当∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

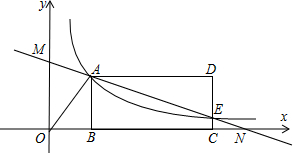    13．如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象经过线段OA的端点A，O为原点，作AB⊥x轴于点B，点B的坐标为（3，0），tan∠AOB=$\frac{4}{3}$．
    （1）求k的值；
    （2）将线段AB沿x轴正方向平移到线段DC的位置，反比例函数y=$\frac{k}{x}$（x＞0）的图象恰好经过DC上一点E，且DE：EC=3：1，求直线AE的函数表达式；
    （3）若直线AE与x轴交于点，N，与y轴交于点M，请你探索线段AM与线段NE的大小关系，写出你的结论并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．在一个不透明的盒子中装有m个除颜色外完全相同的球，这m个球中只有3个红球，从中随机摸出一个小球，恰好是红球的概率为$\frac{1}{5}$，那么m的值是15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

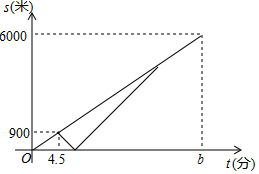    10．周末，甲、乙两名大学生骑自行车去距学校6000米的净月潭公园，两人同时从学校出发，以a米/分的速度匀速行驶，出发4.5分钟时，甲同学发现忘记带学生证，以1.5a米/分的速度按原路返回学校，取完学生证（在学校取学生证所用时间忽略不计），继续以返回时的速度追赶乙，甲追上乙后，两人以相同的速度前往净月潭，乙骑自行车的速度始终不变，设甲，乙两名大学生距学校的路程为s（米），乙同学行驶的时间为t（分），s与t之间的函数图象如图所示．
    （1）求a，b的值；
    （2）求甲追上乙时，距学校的路程；
    （3）当两人相距500米时，直接写出t的值是5.5分钟或17.5分钟．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

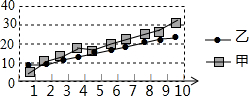    17．某赛季甲、乙两面运动员各参加10场比赛，各场得分情况如图，下列四个结论中，正确的是（　　）
    A．甲得分的平均数小于乙得分的平均数
    B．甲得分的中位数小于乙得分的中位数
    C．甲得分的方差大于乙得分的方差
    D．甲得分的最小值大于乙得分的最小值

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知直线AB的解析式为：y=2x-4，
    （1）当y＞-4时，求x得取值范围；
    （2）当-2≤x≤4时，求y的取值范围；
    （3）已知存在另一直线CD，其解析式为：y=3x+m，若直线AB，CD交于点E，且E在第四象限，求此时m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

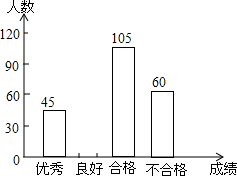    15．为了解今年初三学生的数学学习情况，某校对上学期的数学成绩作了统计分析，绘制得到如下图表．请结合图表所给出的信息解答下列问题：
    成绩频数频率
    优秀45b
    良好a0.3
    合格1050.35
    不合格60c
    （1）该校初三学生共有多少人？
    （2）求表中a，b，c的值，并补全条形统计图．
    （3）初三（一）班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率．

    查看答案和解析>>

    同步练习册答案