
 如图所示,E是正方形ABCD的边BC上一点,F是DC的延长线上一点,且∠BAE=∠FAE,求证:BE+DF=AF.
如图所示,E是正方形ABCD的边BC上一点,F是DC的延长线上一点,且∠BAE=∠FAE,求证:BE+DF=AF.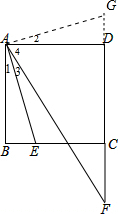
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 下列是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,填空.
下列是胡老师带领学生,探究SSA是否能判定两个三角形全等的过程,填空.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| m-3 |
| 1 |
| m+3 |
| 2m |
| m2-6m+9 |
| 1 |
| x |
| 1 |
| y |
| 2x-14xy-2y |
| x-2xy-y |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
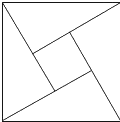 2002年8月在北京召开的国际数学家大会的会徽取材于我国古代数学家赵爽的《勾股圆方图》它是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形,如图,若大正方形的面积是64,一个直角三角形两直角边长和为10,则小正方形的面积为
2002年8月在北京召开的国际数学家大会的会徽取材于我国古代数学家赵爽的《勾股圆方图》它是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形,如图,若大正方形的面积是64,一个直角三角形两直角边长和为10,则小正方形的面积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com