
【题目】如图,y=﹣x2+mx+3(m>0)与y轴交于点C,与x指的正半轴交于点k,过点C作CB∥x轴交抛物线于另一点B,点D在x轴的负半轴上,连结BD交y轴于点A,若AB=2AD.
(1)用含m的代数式表示BC的长;
(2)当m=2时,判断点D是否落在抛物线上,并说明理由;
(3)过点B作BE∥y轴交x轴于点F,延长BF那至E,使得EF=![]() BC,连结DE交y轴于点G,连结AE交x轴于点M,若△DOG的面积与△MFE的面积之比为1:2,则求出抛物线的解析式.
BC,连结DE交y轴于点G,连结AE交x轴于点M,若△DOG的面积与△MFE的面积之比为1:2,则求出抛物线的解析式.
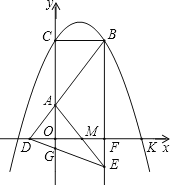
【答案】(1)BC=m;(2)当m=2时,点D落在抛物线上;(3)y=﹣x2+x+3.
【解析】
(1)因为抛物线的对称轴为x=![]() ,由对称性即可得出BC的长;
,由对称性即可得出BC的长;
(2)当m=2时,BC=2,由题意,可得△AOD∽△ACB,利用相似三角形对应边成比例求得点D(﹣1,0),即可判断点D是否落在抛物线上;
(3)由△AOD∽△ACB,求得A(0,1),D(﹣![]() ,0),因为点E(m,﹣
,0),因为点E(m,﹣![]() ),用待定系数法分别求得直线AE,DE的表达式,即可得出点M,点G的坐标,根据△DOG的面积与△MFE的面积之比为1:2,列出方程,解方程即可求得m的值.
),用待定系数法分别求得直线AE,DE的表达式,即可得出点M,点G的坐标,根据△DOG的面积与△MFE的面积之比为1:2,列出方程,解方程即可求得m的值.
(1)∵y=﹣x2+mx+3(m>0).
∵抛物线的对称轴为x=![]() ,
,
∴BC=m.
(2)当m=2时,BC=2,y=﹣x2+2x+3
∵CB∥x轴,
∴△AOD∽△ACB,
∴DO:BC=AD:AB=1:2,
∴DO=1,即点D(﹣1,0),
当x=﹣1时,y=﹣(﹣1)2+2×(﹣1)+3=0,
∴当m=2时,点D落在抛物线上;
(3)∵过点B作BE∥y轴交x轴于点F,延长BF至E,使得EF=![]() BC,
BC,
∴点E(m,﹣![]() ).
).
∵C(0,3),OD:BC=OA:AC=AD:AB=1:2,
∴OA=1,OD=![]() ,
,
∴A(0,1),D(﹣![]() ,0),
,0),
设直线AE表达式为y=kx+b,把E(m,﹣![]() ),A(0,1)代入得
),A(0,1)代入得
∴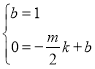 ,
,
解得: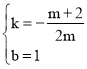 ,
,
∴直线AE表达式为y=﹣![]() x+1,
x+1,
∴点M坐标为(![]() ,0),
,0),
设直线DE表达式为y=ax+t,
将D(﹣![]() ,0),E(m,﹣
,0),E(m,﹣![]() )代入得
)代入得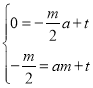 ,
,
解得: ,
,
∴直线DE表达式为y=﹣![]() x﹣
x﹣![]() ,
,
∴点G坐标为(0,﹣![]() ).
).
∵△DOG的面积与△MFE的面积之比为1:2,
∴2×![]() ×
×![]() ×
×![]() =
=![]() ×
×![]() ×(m﹣
×(m﹣![]() ).
).
∵m>0,∴m=1.
故该抛物线解析式是:y=﹣x2+x+3.


科目:初中数学 来源: 题型:
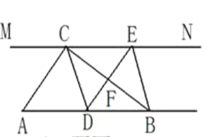
【题目】如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由
(3)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
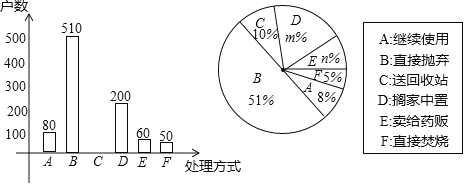
【题目】家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某市药监部门为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调査.
(1)下列选取样本的方法最合理的一种是 .(只需填上正确答案的序号)
①在市中心某个居民区以家庭为单位随机抽取;②在全市医务工作者中以家庭为单位随机抽取;③在全市常住人口中以家庭为单位随机抽取.
(2)本次抽样调査发现,接受调査的家庭都有过期药品,现将有关数据呈现如图:
①m= ,n= ;
②补全条形统计图;
③扇形统计图中扇形C的圆心角度数是 ;
④家庭过期药品的正确处理方式是送回收点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.
查看答案和解析>>
科目:初中数学 来源: 题型:
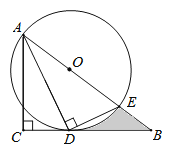
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:直线BC是⊙O的切线;
(2)若∠ABC=30°,⊙O的直径为4,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
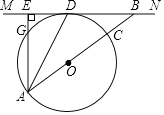
【题目】如图,AC为⊙O的直径,MN为⊙O的切线,点D为切点,连结AD.直线MN与直线AC交于点B,过点A作AE⊥MN,垂足为E.
(1)求证:AD平分∠EAB.
(2)求证:AD2=AGAB.
(3)若AE=6![]() ,BE=8
,BE=8![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设天府新区“公园城市”,实现城市生活垃圾减量化、资源化、无害化的目标.近日,成都市天府新区计划在各社区试点实施生活垃圾分类处理活动,取得市民积极响应.某创业公司发现这一商机,研发生产了一种新型家庭垃圾分类桶,并投入市场试营销售.已知该新型垃圾桶成本为每个40元,市场调查发现,该垃圾桶每件售价y(元)与每天的销售量为x(个)的关系如图.为推广新产品及考虑每件利润因素,公司计划每天的销售量不低于1000件且不高于2000件.
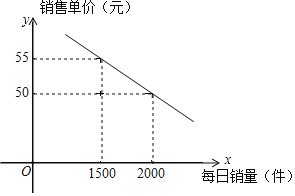
(1)求每件销售单价y(元)与每天的销售量为x(个)的函数关系式;
(2)设该公司日销售利润为W(元),求每天的最大销售利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com