
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
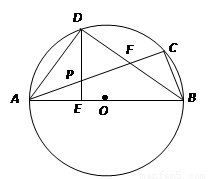
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
(1)见解析(2)见解析(3)见解析
【解析】
试题分析:(1)利用等弧对等弦即可证明.
(2)利用等弧所对的圆周角相等,∠BAD=∠CBD再等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以B,E,C三点在以D为圆心,以DB为半径的圆上.
(3)利用等弧所对的弦相等,得出AD的长度,再根据勾股定理得出AB的长度,然后得出园的半径,再根据相似直角三角形对应对成比例竿出DE的长度.
解:(1)∵BD平分∠CBA,∴∠CBD=∠DBA
∵∠DAC与∠CBD都是弧CD所对的圆周角,∴∠DAC=∠CBD
∴ ∠DAC =∠DBA
∵AB为直径,
∴∠ADB=90°
∠DAC =∠DBA
∵AB为直径,
∴∠ADB=90°
又∵DE⊥AB于点E,∴∠DEB=90°
∴∠ADE +∠EDB=∠ABD +∠EDB=90°
∴∠ADE=∠ABD=∠DAP
∴PD=PA ………………………………………………4分
(2)A,D,F三点在以P为圆心,以PD为半径的圆上
∵∠DFA +∠DAC=∠ADE +∠PD F=90°且∠ADE=∠DAC
∴∠PDF=∠PFD
∴PD=PF ∴PA=PD= PF
即 A,D,F三点在以P为圆心,以PD为半径的圆上…………….8分
(3)⊙O的半径是2.5;DE的长是2.4
考点:确定圆的条件;圆心角、弧、弦的关系;勾股定理.
点评:本题主要考查等弧对等弦,及确定一个圆的条件,此类题是中考的常考题,需要同学们牢固掌握.


科目:初中数学 来源: 题型:
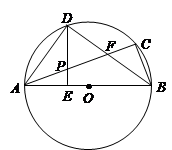
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.

1.求证:∠DAC =∠DBA;
2.求证:![]() 是线段AF的中点
是线段AF的中点
3.若⊙O 的半径为5,AF =![]() ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
 是线段AF的中点
是线段AF的中点 ,求tan∠ABF的值.
,求tan∠ABF的值.查看答案和解析>>
科目:初中数学 来源:2012届江苏苏州九年级中考模拟数学试卷(带解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 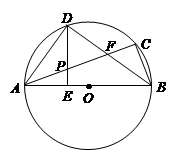
【小题1】求证:∠DAC =∠DBA;
【小题2】求证: 是线段AF的中点
是线段AF的中点
【小题3】若⊙O 的半径为5,AF =  ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
科目:初中数学 来源:2013届湖北宜城九年级上学期期中考试数学试卷(有解析) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:AP=PD;
(2)请判断A,D,F三点是否在以P为圆心,以PD为半径的圆上?并说明理由;
(3)连接CD,若CD﹦3,BD ﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏苏州九年级中考模拟数学试卷(解析版) 题型:解答题
已知:如图,DABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
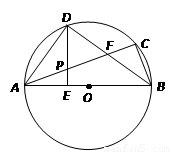
1.求证:∠DAC =∠DBA;
2.求证: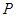 是线段AF的中点
是线段AF的中点
3.若⊙O 的半径为5,AF =
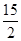 ,求tan∠ABF的值.
,求tan∠ABF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com